Osnove

Zadatak otpornosti materijala je da utvrdi koje spoljne sile može da izdrži čvrsto telo (napr., građevina, konstruktivni deo ili zemljište). Da bi se dao odgovor na ovo pitanje polazi se od dva kriterijuma: s jedne strane naponi, ne smeju da prekorače izvesne granice koje zavise od vrste materijala, a s drugr strane ravnoteža između spoljnih i unutrašnjih sila mora da bude stabilna. U skladu sa ovim, svi problemi otpornosti materijala mogu se podeliti na "Probleme napona" i "probleme stabilnosti. 

Kod štapova i greda i od njih sastavljenih nosača (rešetke, okviri) određivanje napona vrši se u dva koraka, i to na taj način što se prvo na osnovu zadatih spoljnih sila izračuna rezultanta unutrašnjih sila koje se prenose preko poprečnog preseka, a zatim se iz ovih "presečnih sila" određuju naponi. Prvi deo postupka predstavlja posebnu, obimnu disciplinu, statiku građevinskih konstrukcija, koja ima razrađene sopstvene metode i koja se obično odvaja od otpornosti materijala , čiji se zadatak svodi na određivanje napona iz datih presečnih sila.

Osnovni pojmovi otpornosti materijala

Do definicije napona dolazi se putem sledećih osnovnih razmatranja. Neka na telo deluje ravnotežni sistem spoljnih sila. Zamislimo da smo telo proizvoljnim presekom podelili na dva dela, i da smo jedan od njih uklonili zajedno sa silama koje na njega deluju; tada se njegovo delovanje na drugi deo, da bi na ovorne ravnoteža sila i raspored deformacija ostali nepromenjeni, moraa zameniti dopunskim silama koje se prenose preko površine preseka. Ove "unutarnje" sile su neprekidno raspoređene po povrsini preseka, tako da svakom elementu površine dF odgovara sila dβ. Ako se obrazuje količnik dβ dF i načini granični prelaz dF -> 0, tada ovaj količnik teži grraničnoj vrednosti koji se naziva napon. Napon u pdređenom elementu površine je, kao i dβ, i može se razložiti na komponenete normalnu i tangencijalnu na dF, normalni napon σ smičući napon τ. 

Ako se kroz istu tačku povuku preseci u različitim pravcima, njima će odgovarati i različiti naponi. Posebno ako se iz tela izdvoji elementarni kvadar, prikazan na sl. 1, u svakoj od njegovih šest površina delovaće vektor napona koji se može razložiti na tri komponente u pravcu koordinatnih osobina x, y z. Naponi koji deluju na naspramne strane površine razlikuju se međusobno, naravno, samo za diferencijal, tako da treba razlikovati 3 * 3 = 9 komponentalnih napona, koji se obeležavaju na sledeći način:

Normalnim naponima σ daje se indeks osovine u čijem pravcu leže i smatraju se pozitivnim ako izazivaju zatezanje, negativnim, ako izazivaju pritisak. Smičući naponi τ dobivaju dva indeksa, prvi je od njih isti kao i indeks odgovarajućeg normalnog napona, a drugi se odnosi na osovinu u pravcu koje smičući napon deluje. Ako je pozitivni smer odgovarajućeg normalnog napona u smeru pozitivne (negativne) koordinatne osovine, i smičući napon se smatra pozitivnim ako deluje u smeru pozitivne (negativne) koordinatne osovine.

 

  Slika 1.

 Konjugovanost smičućih napona

Ako se za elementarni kvadar, sl. 1, postavi uslov da je moment svih sila u odnosu na osovinu x nula, dobija se τ_yz dx dz * dy = τ_zy dx dy * dz Odavde, i iz dveju odgovarajućih jednačina za osovine y i z, dobija se da su smičući naponi sa istim indeksima međusobno jednaki τ_xy = τ_yx, τ_yz = τ_zy, τ_zx = τ_{xz  (1)}

Komponentalne deformacije

Da napred definisani naponi imaju fizički smisao, proizilazi iz njihove veze sa definicijom koju trpi svako telo pod uticajem spoljnih sila. Sl. 2 prikazuje jedan elementarni kvadar, koji je pre deformacije bio pravougaoni i imao dužine ivica dx, dy, dz. Dužine ivica posle deformacije možemo obeležiti sa dx + Δdx, dy, + Δdy, dz + Δdz količnici ε_x = Δdx|dx, ε_y =Δdy|dy, ε_z = Δdz|dz nazivaju se dilatacije. Ovo su veličine bez dimenzije i kod svih materijala koji dolaze u obzir u građevinarstvu male prema 1. Osim izduženja ivica, elementarni kvadar dx * dy * dz može pretrpeti još i promenu prvobitno pravih uglova između njegovih stranica. 

Slika 2. komponentalna deformacija

Neka je posle deformacije ugao između ravni koje se sustiču duž ivice OC jednak  i slično tome neka je smanjenje pravog ugla duž ivice AO jednak γ_yz, i smaanjenje duž ivice OB jednak γ_zx. Ove tri promene uglova γ_xy, γ_yz, γ_zx, nazivaju se klizanja i takođe su uvek male prema 1.  Sa šest komponentalnih ε i γ potpuno je određena deformacija elementarnog kvadera "deformacija u malom". Promena elementa zapremine dV = dx * dy * dz je ΔdV = (dx + Δdx) (dy + Δdy) (dz + Δdz) - dx dy dz, odakle se, kada se zanemare proizvodi dilatacija kao male veličine višeg reda, dobija kubna dilatacija ϱ = ΔdV|dV = ε_x, ε_y, ε_{z (2)}

Pomeranja

 Deformacija čvrstog tela može se potpuno opisati i na taj način, što se za svaku od njegpvih tačaka da pomeranje koje je ta tačka pretrpela. Ako se iz posmatranja isključe pomeranja konačne veličine koja odgovaraju pomeranju krutog tela, na taj način, što se, ako je to potrebno, u računu usvoji pomerljivi koordinatni sistem, tada su i komponentalna pomeranja μ, ν, ω uvek male veličine, a njihovi izvodi prema koordinatama mali prema 1. Pod tom pretpostavkom je prema sl. 3 dužina liniskog elementa OA = dx posle deformacije

 

dakle  (3)

 Na sličan način se iz sl. 3 vidi da je klizanje γxy γ1 + γ2: i takođe 

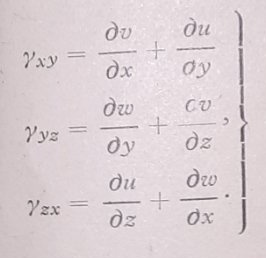  (4)

 

 

Slika 3 klizanje 

 (5)  (6)

Ove veze se nazivaju uslovi kompatibilnosti i iskazuje da se deformisani elementi mogu uklopiti kao mozaik tako da pri tome prostor bude neprekidno ispunjen, što se ne može postići ako su deformacije elemenata proizvoljne. Uslovi kompatibilnosti su diferencijalne jednačine, pa su, razume se, svih šest komponentalnih deformacija za svaki pojedini kvadar međusobno nezavisne, ali je njihov raspored u svakoj konačno rasprostrtoj oblasti vezan uslovima (5) i (6). 

Pošto su ovi uslovi dobiveni diferenciranjem iz jednačina (3) i (4), prilikom njihovog izvođenja gubi se deo veza sadržanih u prvobitnim jednačinama. Zato nije dovoljno da bude ispunjen samo jedan od ova dva sistema jednačina, već se moraju zadovoljiti oba sistema jednačina, ako se želi da kompatibilnost deformacije bude obezbeđen. 

Diferencijalne jednačine sistem elastičnosti

Za izračunavanje napona i deformacija kod elastičnih tela služe sledeće jednačine: 

Uslovi ravnoteže zapreminskog elementa. Uslovi da su momenti oko tri osovine jednaki nuli iskorićeni su već pri izvođenju jednačine (1). Uslovi ravnozeža sila daju prema sl. 4

 

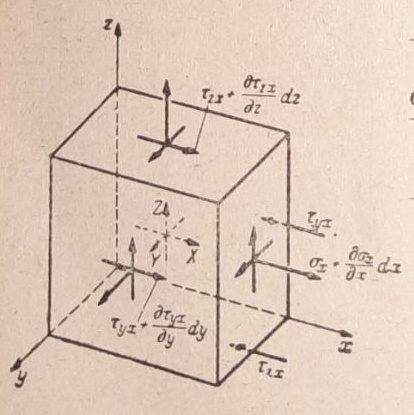
Slika 4

(7a-c)

Ako se sa X, Y, Z označe komponente zapreminskih sila (npr. težina, centrifugalna sila) na jedinicu zapremine. Veze između napona i deformacija. Pod ovim se podrazumeva veza između komponentalnih napona i komponentalnih deformacija. U teoriji elastičnosti po pravilu dolazi u obzir samo linearna veza, koja se iskazuje Hooke-ovim zakonom: 

 

(8a-c)

(8d-f)

 Ako se jednačine (8a-c) reše po naponima, dobija se

(8 a)

kso i dve odgovarajuće jednačine. Hooke-ov zakon iskazan jednačinom (8) ne pretstavlja neki strogo ispunjen prirodni zakon, nego idealizaciju stvarnog ponašanja, koje od njega otstupa više ili manje, u zavisnosti od materijala i od veličine naprezanja. S obzirom na to da matematička obrada problema otpornosti materijala sa komplikovanim, nelinearnim vezama između napona i deformacija pričinjava neuporedivo veće teškoće i može se stvarno sprovesti samo u najprostijim slučajevima, moraju se i kod onih materijala (beton!) čije ponašanje znatno otstupa od Hooke-ovog zakona, proračuni zasnovani na njemu koristiti kao prvo, i većinom i jedino približno rešenje, koje je uostalom po pravilu vrlo upotrebljivo i da je uvid koji je više nego samo kvalitativan. G = E|2 (1+μ).

Ona nužno sleduje iz veze između napona i deformacije (8), iz jednačina transformacije (16) za napone i odgovarajućeg sistema jednačina za komponentalne deformacije E i G imaju dimenziju napona i kod svih građevinskih materijala su veliki prema naponima σ i τ koji se mogu pojaviti. No ovoj činjenici počiva pretpostavka usvojena svuda u teoriji elastičnosti, da su deformacije male. Koeficijent poprečne dilatacije (Poisson-ov broj) μ je bez dimenzije i nalazi se uvek između 0 i ¹/₂ .

Veze između komponentalnih deformacija i pomeranja. Ove veze date su jednačinama (3), (4). One su čisto geometriske prirode. Ova tri sistema daju 3+6+6=15 jednačina za 15 nepoznatih, tj. za 6 komponentalnih napona, 6 komponentalnih deformacija i 3 komponentalna pomeranja. One su prema tome dovoljne za određivanje ovih nepoznatih. Matematičko savlađivanje ovako obimnog sistema diferencijalnih jednačina moguće je, razume se, samo u specijalnim slučajevima. Ako se u jednačini (8) komponentalne deformacije zamene komponentalnim pomeranjima prema jednačinama (3) i (4) i zatim normalni naponi σ i smičući naponi τ,prema jednačinama (8 d - f), uvedu u uslove ravnoteže, jedn. (7), dobijaju se diferencijalne jednačine koje se nazivaju osnovne jednačine teorije elastičnosti. 

 

(9)

 pri čemu je 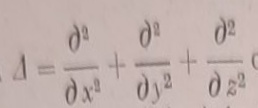 označen Laplace-ov operator. S obzirom na (2) ovo su tri diferencijalne jednačine sa tri komponentalna pomeranja μ, ν, ω; iz ovih se pak diferenciranjem na osnovu (3), (4) i (8) mogu dobiti svi komponentalni naponi i deformacije. Jednačine (9) pretstavljaju često pogodnu polaznu tačku za proučavanje specijalnih slučajeva.

Deformacioni rad

Definicija

Kada se nosač optereti, napadne tačke spoljnih sila trpe elastična pomeranja i sile vrše pri tome izvestan rad. Na ovaj način dovedena energija može da pređe u različite oblike. ‚Ako se opterećenje na ese naglo, tako da proces deformacije ima znatnu brzinu, jedan deo ove energije pretvara se u kinetičku energiju, koja se tokom vremena rasipa, bilo na taj način što se prenese na tle kao elastični talas koji se gubi u beskonačnosti, bilo što se unutarnjim trenjem pretvara u toplotu. Ako se tereti nanose tako lagano da pri tome ne nastaje primetan priraštaj kinetičke energije, dakle, da su tereti koji postepeno rastu počevši od nule u stalnoj ravnoteži sa unutarnjim silama, energija se očigledno isključivo troši na deformisanje tela i tada se naziva deformacioni rad.

 Proračunavanje deformacionog rada prikazaćemo najpre na deliću opterećenom na zatezanje u jednom pravcu (sl. 5).

Neka se postojeći napon σ i odgovarajuća dilatacija ε pretrpe priraštaje dσ i dε. Tada će sila σdF na putu dε * dl izvršiti rad  σdF * dεdl = σdεdV, ako se za dV označi zapremina delića. Ako napon raste od nule do svoje konačne vrednosti i dilatacija u skladu sa tim od 0 do ε, ukupno izvršeni rad po jedinici zapremine iznosiće:

Slično tome je i za element opterećen smičućim naponom τ (sl. 6) deformacioni rad na jedinicu zapremine (specifični deformacioni rad, elastični potencijal):

pri čemu samo jedna od četiri sile τ * dF vrši rad. 

U opštem slučaju, kada na elementarni delić napadaju svih šest komponentalnih napona, dobija se specifični deformacioni rad sabiranjem radova pojedinih komponentalnih napona:

(10)

Diferenciranjem po gornjoj granici svakog od ovih integrala dobijaju se odnosi koji važe u najopštijem slučaju:

(11)

i slično za ostale komponentalne deformacije. Ako je telo elastično, svakom odredjenom stanju napona odgovara uvek isto stanje deformacije, bez obzira da li je stanje dostignuto prilikom opterećenja ili rasterećenja. Tada pod integralima stoje jednoznačne funkcije i ukupna energija utrošena prilikom opterećenja i zatim potpunog rasterećenja je a = 0, s obzirom na to da u ovom slučaju gornje granice integrala postaju nula. Prema tome ukupna energija dovedena telu prilikom opterećenja dobija se natrag prilikom rasterećenja.

 

Slika 6

Slika 7

Za nepotpuno elastično telo veza između napona i deformacija za ceo ciklus opterećenja i rasterećenja ima oblik približno prikazan na sl. 7 linijama O A B. Energija  dovedena pri opterećenju jednaka je površina OAA, a energija vraćena priliko rasterećenja površina ABA, tako da se gubi (pretvara u toplotu) rad koji odgovara šrafiranoj površini. Ako se u oscilaatornom procesu napon periodično menja između pozitivne granične vrednosti  i negativne granične vrednosti,  neelastična deformacija teče sličnotome kako jr prikazano isprekidanimlinim linijama na sl. 7 i prilikom svake periode oscilacije pretvara se po jedinici zapremine u toplotu energija DABCD. Takvo ponašanje prilikom deformacije, pri kome deformacija yaostaje za naponom, naziva se elastični histeresis, a kriva DABCD petlja histeresisa. 

Deformacioni rad i Hooke-ov zakon

Ako sc u integrale u jednačini (10) uvede Hooke-ov zakon, može se izvršiti intcgriranje, pa se za specifični deformacioni rad dobijaju izrazi:

(12a)

(12b)

(12c)

Ako se drugi od ovih oblika unese u jednačinu (11), dobija se opet Hooke - ov zakon, jednačine (8), u obliku rešenom po naponima. Iskaz da defrmacioni rad zavisi od komponentalmh deformacija, onako kako je prikazano jednačinom (12b), je prema tome ekvivalentan Hooke-ovom zakonu. Kada se jednačina (12c) diferencira po naponima, dobija se

(13)

Ovi obrasci, za razliku od obrazaca (11), važe samo za tela koja se ponašaju prrema Hooke-ovom zakonu i ne mogu se primeniti kada su veze izmedu napona i deformacija drukčije. Razume se da se na desnoj strani jednačina (13) nalaze samo komponentalne deformacije izazvane naponima, a iskijučuju se sve ostale koje su eventualno mogle nastati usled promene temperature, puženja, bubrenja, rekristalizacije, itd.

INTEGRALNI STAVOVI U TEORIJI ELASTIČNOSTI

Virtualna pomeranja. Princip o minimumu potencijalne energije

Kao što se Hooke-ov zakon, jednačine (8) može zameniti jednom jednačinom (12b), tako se i umesto uslova ravnoteže može uvesti princip virtualnih pomeranja, kao opšte važeći osnovni zakon mehanike. Ovaj zakon iskazuje da se ravnotežna stanja odlikuju time što je kod njih ukupno izvršeni rad svih sila pri maloj promeni stanja deformacija jednak nuli. Ako male promene elastićnih pomeranja označimo δμ δν, δω, tada zaprerninske sile definisane jednačinom (7) vrše virtualan rad

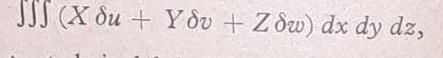
a površinske sile p_x, p_y, p_z koje deluju na element dF spoljne površine tela rad 

pri čemu se trostruki integral odnosi na čitavu zapreminu, a dvostruki na čitavu spoljnu površinu tela. Za sračunavanje rada koji vrše unutarnje sile koristi se jednačina (12b), pa se za rad po jedinici zapremine dobija

Princip virtualnih pomeranja na osnovu toga daje

(14)

Ako se opterećenja X, Y, Z p_x, p_y., p_z shvate kao komponente sile teže (sopstvena težina i spoljno opterečenje), integrali na desnoj strani pretstavljaju potencijalnu energiju koju su ovi tereti izgubili, dok leva strana pretstavlja priraštaj potencijalne (elastične) energije tela, tako da ovaj princip iskazuje da ukupna potencijalna energija nosačea i tereta koji na njemu leže u slučaju ravnoteže ima ekstremnu vrednost. Aka je ova ekstremna vrednost minimum, ravnoteža je stabilna.

Princip o minirnumu potencijalne energije iskazan jednačinom (14), izraz (12b) za deformacioni rad uslovi kompatibilnosti deformacija (5), (6) pretstavijaju sisterm jednačina koji je dovoljan za izgradnju teorije elastienosti, i koji je u osnovi ekvivalentan sistemu jednačina. Ovaj sistem može biti naročito koristan u slučajevima kada zadovoljavanje diferencijalnih, jeclnačina (9) pretstavlja računske teškoće i zbog toga Mora da se traži približno rešenje, napr., za pomeranja unapred pretpostavi pogodnom obliku koji sadrži nekoliko slobodnih konstanata pa se ove određuju iz zahteva da jednačina (14) bude zadovoljena. Tako se doduše ne dobija strogo rešenje problema, nego samo najbolja aproksimacija koja se može postići sa izabranim oblikom rešenja. Da li je približavanje dovoljno, zavisi u prvom redu od usvojenog oblika rešenja, i uspešna primena ove metode zahteva zbog toga spretnost i iskustvo.

Castigliano-v princip

Dok se kod principa o minimumu potencijalne energije upoređuju sva stanja deformacije koja ispunjavaju uslove kompatibilnosti deformacija i izmedu njih izdvajaju ona za kcja odgovarajući naponi zadovoljavaju uslove ravnoteže, kod Castigliano-vog principa uporeduju se sva stanja napona koja zadovoljavaju uslove ravnoteže i izmedu njih se izdvajaju ona za koja odgovarajuće deformacije zadovoljavaju uslove kompatibilnosti deformacija. Ovaj princip glasi: od svih rnogućih ravnotežnih stanja nastupa stvarno ono kome odgovara najmanji deformacioni rad. Castigliano-v princip zajedno sa jednačinom (12c) za deformacioni rad i uslovima ravnoteže obrazuje sistem jednačina koji je dovoljan za izgradnju otpornosti materijala. S obzirom na to da ovaj princip sadrži Hooke-ov zakon mogućnost njegove prirnene je vezana za pretpostavku da se deformacije mogu Potpuno opisati ovim zakonom. Ovo zahteva ne samo linearno elastično ponašanje materijala, već i isključuje promene temperature.

Ponašanje materijala iznad granica elastičnosti

Pojave pri statičkom opterećenu

Deformacija materijala pod uticajem napona je veoma komplikovana pojava, tako da se mora u različitim pravcima uprostiti da bi se mogla razumeti. Jedno od ovih uprošćenja je pretpostavka da se tereti nanose postepeno, kao što se to, napr., radi sa uzorcima prilikom opita na zatezanje i pritisak.

Ako se čelični štap opterćen na zatezanje izloži opterećenju koje postepeno raste i meri njegova dilatacija ε, dobija se dijagram prikazan na sl. 8. U početku je dilatacija veoma mala i proporcionalna naponu, onako kako to zahteva Hook-eov zakon. Počev od jednog određenog napona prestaje proporcionalnost i dilatacija raste brže. Tačan položaj granice ove proporcionalnosti teško se može odrediti. Što je merenje tačnije, utoliko se ona dobija niža. Za većinu materijala ona leži na σ = 0, i Hook-eov zakon pretstavlja tada samo prvo približenje elastičnom ponašanju, prvi član razvitka u Taylor-ov red funkcije ε = ε (σ) u okolini koordinatnog početka. 

Ako se štap rastereti, primećuje se da, kada napon nije bio suviše veliki, nestaje i deformacija, u skladu sa Hook-eovim zakonom. Ali i ovo se menja ako se prekorači izvestan napon koji leži blizu granice proporcionalnosti, tzv. granica elastičnosti; tada se ukupna deformacija sastoji iz elastičnog (povratnog) i neelastičnog (trajnog) dela. Ni granica elastičnosti ne može se tačno odrediti, ona se nalazi utoliko niže ukoliko je tačnost merenja veća. Međutim, kako ona ima veliki tehnički značaj, jer pretstavlja granicu važnosti kod skoro svih proračuna u otpornosti materijala, a istovremeno i granicu na kojoj nastaju prva trajna oštećenja, ona se za ispitivanje uzoraka oštro definiše nekom usvojenom konvencijom, pa se, napr, kao granica 0.2% označava onaj napon pri kome trajna dilatacija dostiže 0.2%.

 Neposredno po prekoračenju granice elastičnosti deformacija naglo raste i može se primetiti golim okom; pri skoro konstantnom naponu štap se neprekidno izdužuje. Ovaj napon se naziva granica tečenja. Kod hidrauličkih mašina za ispitivanje materijala može se uz to zapaziti posle početka tečenja više ili manje izražen pad napna; kako je naznačeno na sl. 8 isprekidanom krivom; tada se maksimum naziva gornja granica tečenja, a konstantni napon tečenja koji zatim nastupa donja granica tečenja.

Pošto se dostigne određena dilatacija, koja je skoro potpuno neelastična, napon počinje ponovo da raste‚, materijal učvršćava. U ovoj oblasti opterećenja nastaje primetno smanjenje poprečnog preseka štapa usled (neelastične) bočne kontrakcije, i dalji tok dijagrama napona i deformacija zavisi u prvom redu od toga da li se pri računanju napona σ sila zatezanja P koja deluje na štap deli sa prvobitnim presekom F₀ ili trenutnim presekom F. Za tehničke svrhe interesantan je napon P|F₀ . Ovaj napon prolazi kroz maksimum koji se naziva jačina materijala i kada se taj maksimum prođe, štap se na jednom mestu jako sužava i kida. "Stvarni napon" P|F raste do sloma. 

Slika 8.

Ponašanje drugih metatala u mnogome otstupa od ovde opisanog. Tečenje često nije izraženo, a očvršćenje počinje neposredno posle prekoračenja granice elastičnosti. Kod krtih materijala (kamen, staklo, beton) neelastične deformacije su uopšte male i već kod male dilatacije dolazi do sloma. Ukupna dilatacija koju materijal pretrpi do sloma je mera istegljivosti (suprotno: krtosti) materijala i ona se za čelik tačno propisuje u tehničkim uslovima. Međutim, kako se neposredno pre sloma dalja deformacija koncentriše na okolna mesta suženog preseka dobija se različita vrednost dilatacije pri slomu, prema tome da li se za mernu dužinu usvaja veći ili manji deo štapa, tako da se za dobijanje jednoznačnih i međusobno uporedivih rezultata mora unapred usvojiti neka određena konvencija. Dilatacija pri slomu po pravilu se meri tako što se na okruglom štapu prečnika d pre opita označi merna dužina Ι = 10 d i iz njenog izduženja ΔΙ sračuna dilatacija pri slomu εsΙ = ΔΙ|Ι . Ako je potrebno da se ispituju štapovi drukčijeg preseka, merna dužina određuje se prema prečniku kružnog cilindričnog štapa koji ima istu površinu poprečnog preseka. 

Dugotrajno opterećenje

Za tok opita zatezanja prilično je svejedno, da li se opterećenje do sloma povećava u toku 10 minuta ili nekoliko sati. Međutim, ako opterećenje deluje godinama ili desetinama godina, pod izvesnim uslovima primećuje se da i ispod granice tečenja deformacija pri konstantnim naponom tokom vremena lagano raste. Pri tome se elastični deo, tj. onaj deo koji pri konačnom rasterećnju nestaje, ne menja osetno. Ovaj porast neelastične deformacije koji se događa tokom dueg vremena naziva se puženje. Kod metala, osim kod olova, puženje je od značaja samo na visokim temperaturama, međutim, za građevinskog inženjera ono igra ulogu kod betona koji pod pritiskom lagano popušta, tako da napon raste u pritisnutoj armaturi, ako ova postoji. 

Promenljivo opterećenje

 

Da bi se Mehaničke karakteristike materijala, dobivene pri opitu na zatezanje, moglo prirneniti kao merilo za dozvoljeno opterećenje konstrukcija, uslov je da materijal pri svakom ponovnom opterećenju podnosi napon koji je jednom bez ogštećenja podneo. Ovaj uslov nije ispunjen ako je materijal izložen čestom ponavljanju opterećenja i rasterećenja, kao što je to, napr., slučaj kod nosača opterećemih inercijalnim silama nepotpuno izbalansiranih mašina. Dovoljno čestim ponavljanjem opterećenja može se konstruktivni deo dovesti do sloma i pri naponu koji leži daleko ispod jačine materijala određene običnim statičkim ispitivanjem. Pojava sloma ove vrste naziva se slom usled zamaranja. Broj n ciklusa opterećenja koje materijal može da podnese zavisi od veiličine napona σ, tako da je utoliko veći, ukoliko je manji napon. Tipičan primer ove zavisnosti pokazan je na sl. 9, iz koje se vidi da za jačinu materljala postoji donja granica, koju podnosi i pri proizvoljno velikom broju ciklusa opterećenja i koja se naziva clinamička jačona materijala Dijagrami ove vrste (sl.9) nazivaju se Wӧhler-ove krive.

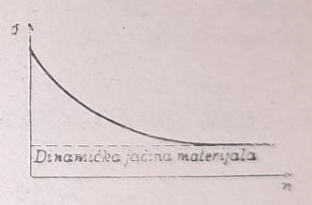
Slika 9.

Sigurnost konstrukcija

Dva granična opterećenja su značajna za konstrukcije: opterećenja pri kome nastaju prva trajna oštećenja (granica tečenja), i opterećenje pri kome je nosivost konstrukcije iscrpna, pa se ona lomi (granica lomljenja). Kako pre granice tečenja bar približno važe pretpostavke otpornossti materijala (mala pomeranja, Hook-eov zakon), sigurnost prema trajnim deformacijama može se pouzdano proceniti u svim onim slučajevima u kojima pođe za rukom da se savladaju matematičke teškoće. Ako je napon proporcionalan opterećenju, odnos napona tečenja prema najvećem naponu koji se u konstrukciji pojavljuje jednak je odnosu između opterećenja pri kome nastaje tečenje i stvarnog opterećenja i pretstavlja koeficijent sigurnosti prema tećenju. Međutim, u nizu slučajeva ovaj jednostavni odnos ne postoji: savijanje kada se isključuje zatezanja, pritisak između ispupčenih površina, sistemi čija je struktura promenljiva i, što je naročito nepogodno, savijanje sa aksijalnom silom. U svim ovim slučajevima može srazmerno malo povećanje opterećenja da dovede do velikog povećanja napona, i tada nije dovoljno da se uobičajeni koeficijent sigurnosti primeni na napone, već se on mora primeniti na opterećenje. 

Pojave koje se desavaju posle prekoračenja granice tečenja do sloma mogu se u većini slučajeva pratiti još samo kvalitativno. Ako je materijal rastegljiv, delovi u kojima je najpre dostignuta granica tečenja, i koji se dalje deformišu pri konstantnom naponu ili naponu koji neznatno raste, učestvuju malo u primanju daljeg opterećenja, tako da ostali, slabije napregnuti delovi konstrukcije ukoliko je to moguće s obzirom na njenu strukturu, više učestvuju u nošenju. U ovoj težnji ka izjednačavanju vrhova napona leži izvesna rezerva sigurnosti, koja se računski može iskoristiti ako trajna deformacija pojedinih delova, nastala pri samo jednom znatnom opterećenju, nije štetna (metoda graničnog opterećenja). 

Ako je materijal krt, prvo trajno oštećenje ispoljava se u prslinama, usled kojih na ugroženom mestu dolazi do još jače koncentracije napona, koja odmah izaziva slom. Slom usled zamaranja i kod rastegljivih materijala ima karakteristike krtog lomljenja. 

 Veze između napona za različite presečne ravni

Jednačine transformacije

Devet komponentalnih napona na sl. 1, vezani su sa tri uslova ravnoteže. Šest preostalih veličina σ_x, σ_y, σ_z τ_xy, τ_yz, τ_zx  mogu, nezavisno jedna od druge, dobiti proizvoljne vrednosti kao što se vidi iz izvođenja diferencijalnih jednačina teorije elastičnosti. Međutim, kada su ove vrednosti zadate, stanje napona u nekoj tački čvrstog tela potpuno je određeno, tj. kada su poznati naponi za tri međusobno upravne ravni, može se jednoznačno i napon za neku četvrtu ravan ravan koja prolazi kroz datu tačku i čija normala ima proizvoljan pravac.

Na sl 10 pokazan je tetraedar OABC čije su tri strane paralelne ravnima koordinatnog sistema x, y, z a četvrta predstavlja neki proizvoljno orijentisani element površine ABC = dF. Da bi se oznacio njegov pravac i pravac napona koji se preko njega prenosi, uvodi se drugi koordinatni sistem, čija je ξ osovina upravna na dF.

Slika 10

 

 Uslov ravnoteža sila koje napadaju na ovaj tetraedar u pravcu ξ osovine daje

Ako se uzme u obzir da je 

dobija se

 i slično tome iz uslova ravnoteže u pravcu osovine η:

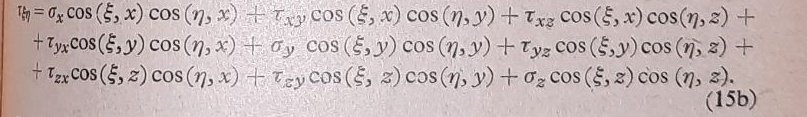
Ovo au jednačine koje služe za proračun napona pri transformaciji koordinata. Od posebnog je značaja da se posmatraju samo takvi elementi površine dF za koje se ξ-osovina poklapa sa z-osovinom. Obrasce za ovaj slučaj možemo dobiti uprošćenjem prethodnih obrazaca ili pročitati neposredno iz sl. 11:

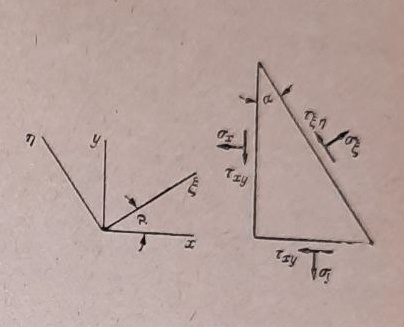
Slika 11

Normalni napon uzima ekstremne vrednosti za pravce α = α₀ , za koje je dσξ/dα = 0. Diferenciranjem se iz jednačine (16) dobija 

 pa je, kada se ovaj izraz izjednači sa nulom

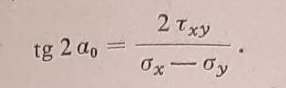
Napon τ_ξη će ujedno biti totalni smičući napon u ovim ravnima, ako je τ_yz = τ_zx = 0. Tada su jednačinom (17) određena dva međusobno upravnapravca za koje: 1. totalni smičući napon je nula i, 2. normalni napon ima ekstremne vrednosti (maksimum i minimum). Ovi pravci se nazivaju pravci glavnih napona, a odgovarajući naponi glavni naponi. Oni se označavaju sa σ₁ i σ₂ i mogu se sračunati neposredno iz obrasca

 Mohr-ov krug

Jednačine (16) mogu se grafički prikazati na očigledan način. U tu svrhu treba ih transformisati na oblik:

Ove jednačine predstavljaju u koordinatnom sistemu σ, τ parametarski oblik jednačine kruga, ucrtanog na sl. 12, čije su koordinate središta σ = ¹/₂ (σ_x + σ_y), τ = 0 i čiji je poluprečnik

Ovaj krug se naziva Mohr-ov krug. Ako sev kroz tačku x povuče prava paralelna sa preseko x =const., preko koga se prenose naponi σ_x, τ_xy ona će seći krug u tački p, koja se naziva pol Mohr-ovog kruga. Svaka prava pξ povučena kroz ovaj pol seče krug u tački ξ koja određuje napone σ_ξ, τ_ξη koji se prenose preko preseka paralelnog sa pξ.

U pogledu znaka smičućih napona pri crtanju Mohr-ovog kruga treba voditi računa da se oni nanose naviše ako imaju pravac pokazan na sl. 12c. Prema tome od dva konjugovana napona τ_xy, τ_yx, jedan je uvek pozitivan, a drugi negativan. 

Graničnim vrednostima σ₁, σ₂ normalnih napona odgovaraju tačke 1 i 2 na krugu, a prave p1 i p2 daju pravce glavnih napona.

Prikazivanje napona koji leže u x-y ravni pomoću Mahr-ovog kruga nije veyano ni za kakvu pretpostavku o naponima σ_z, τ_xz, τ_yz  upravnim na ovu ravan.

Slika 12

Ono prema tome važi i za najopštije trodimenzionalno stanje napona, ako se upoređuju samo one presečne ravni koje sve prolaze kroz istu pravu, koja je ovde izabrana za z i ξ osovinu. Kako prema opštim jednačinama transformacije (15) normalni napon σ ne može da postane beskonačan ni za jednu presečnu ravan, to on mora da ima za neku ravan konačni maksimu σ_1, a za drugu minimum σ₃, od kojih oba, rayume se, mogu da budu i negativni. Ako se kroz vektore σ₁ i σ₃ povuče ravan i nacrta Mohr-ov krug (sl. 13)

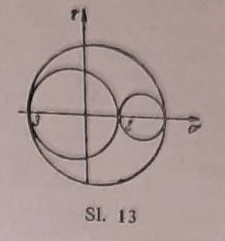
Slika 13

za napone koji leže u ovoj ravni (tj. sve pravce koji upravni na ovu ravan), tada su σ₁ i σ₃ najveći i najmanji normalni naponi koji se mogu pojaviti i prema tome moraju da budu međusobno upravni. Ako se pravci 1 i 3 dopune pravcem 2, tako da ova tri pravca čine pravougli koordinatni sistem, i ako se nacrtaju Mahr-ovi krugovi za ravni 1 ~2 i 2 ~ 3, tada je σ₂ za jedan od ovih krugova najveći, a za drugi najmanji normalni napon, i prema tome je u presecima upravnim na pravce 1, 2 i 3 smičući napon jednak nuli. Tri međusobno upravna normalna napona σ₁, σ₂ i σ₃, kojima ne odgovaraju smičući naponi, nazivaju se glavni naponi.

    Granica tečenja i granica sloma pri prostornom stanju napona

Stanje napona se naziva jedno-, dvo- ili trodimenzionalno, drukčije: linearno, ravno ili prostorno, prema tome da li su jedan, dva ili sva tri glavna napona različiti od nule. Kod konstruktivnih delova koji se najčešće primenjuju, tj. kod zategnutog, pritisnutog i savijenog štapa, stanje napona, bar na najviše napregnutim mestima, je jednodimenzionalno, a isto tako i kod opita na zatezanje, pritisak ili savijanje, koji se pri ispitivanju materijala gotovo isključivo primenjuju za određivanje dozvoljenih napona. Suprotno tome, kod ploča opterećenih u svojoj ravni ili upravno na nju, kao i kod ljuski, stanje napona je dvodimenzionalno, a u izvesnim slučajevima pojavljuju se i trodimenzionalna stanja napona, tako da je potrebno da se na osnovu granice tečenja i sloma, određene pri jednodimenzionalnom stanju napona, izvuku zaključci o ponašanju materijala u slučaju prostornog stanja napona.