Zemljani pritisak na potporne zidove
Zemljana masa koju podupire potporni zid deluje na njega pritiskom, težeći da ga odgura translatorno unapred (sl. 1a) ili da ga preturi (sl. 1b). Veličina zemljanog pritiska E zavisi od više faktora, među kojima su najvažniji fizičke osobine tla, deformacija zida, vlažnost tla i stanje podzemne vode, visina zida, spoljno opterećenje i rapavost unutrašnje površine zida.
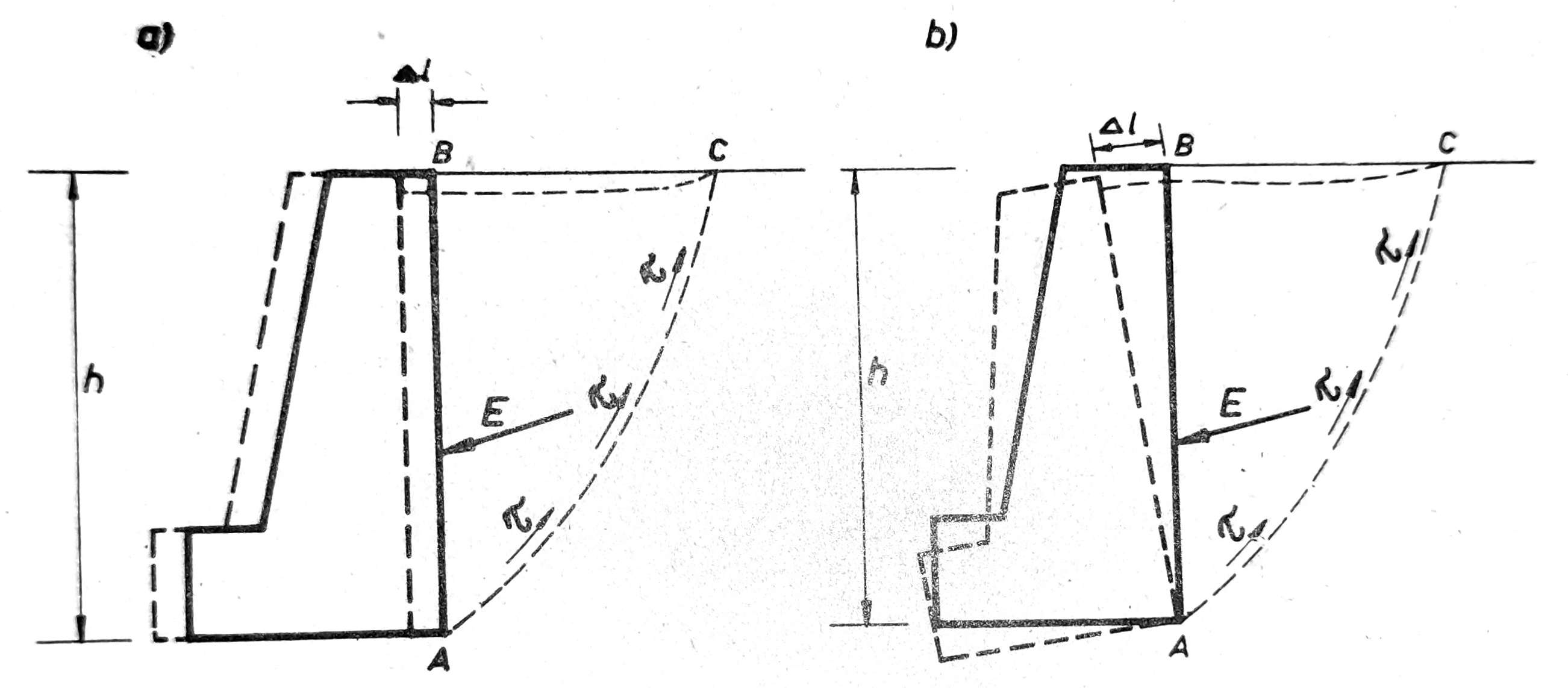
Sl. 1. Zemljani pritisak na potporne zidove
Ako je potporni zid krut i nepokretan, pritisak koji deluje na njega naziva se zemljani pritisak u stanju mirovanja i označuje se sa E0. To je upravo onaj pritisak, koji vlada u neporemećenom tlu na posmatranoj dubini, pod dejstvom sopstvene težine tla i eventualno predopterećenja ranije erodiranih slojeva. Zemljani pritisak u stanju mirovanja je redak i nastupa samo u izvesnim slučajevima, kao što su kod potpornih zidova fundiranih u čvrstoj steni, zatim kod zatvorenih profila tunela i cevi i kod masivnih dokova, koji su potpuno nepokretni (sl. 2).
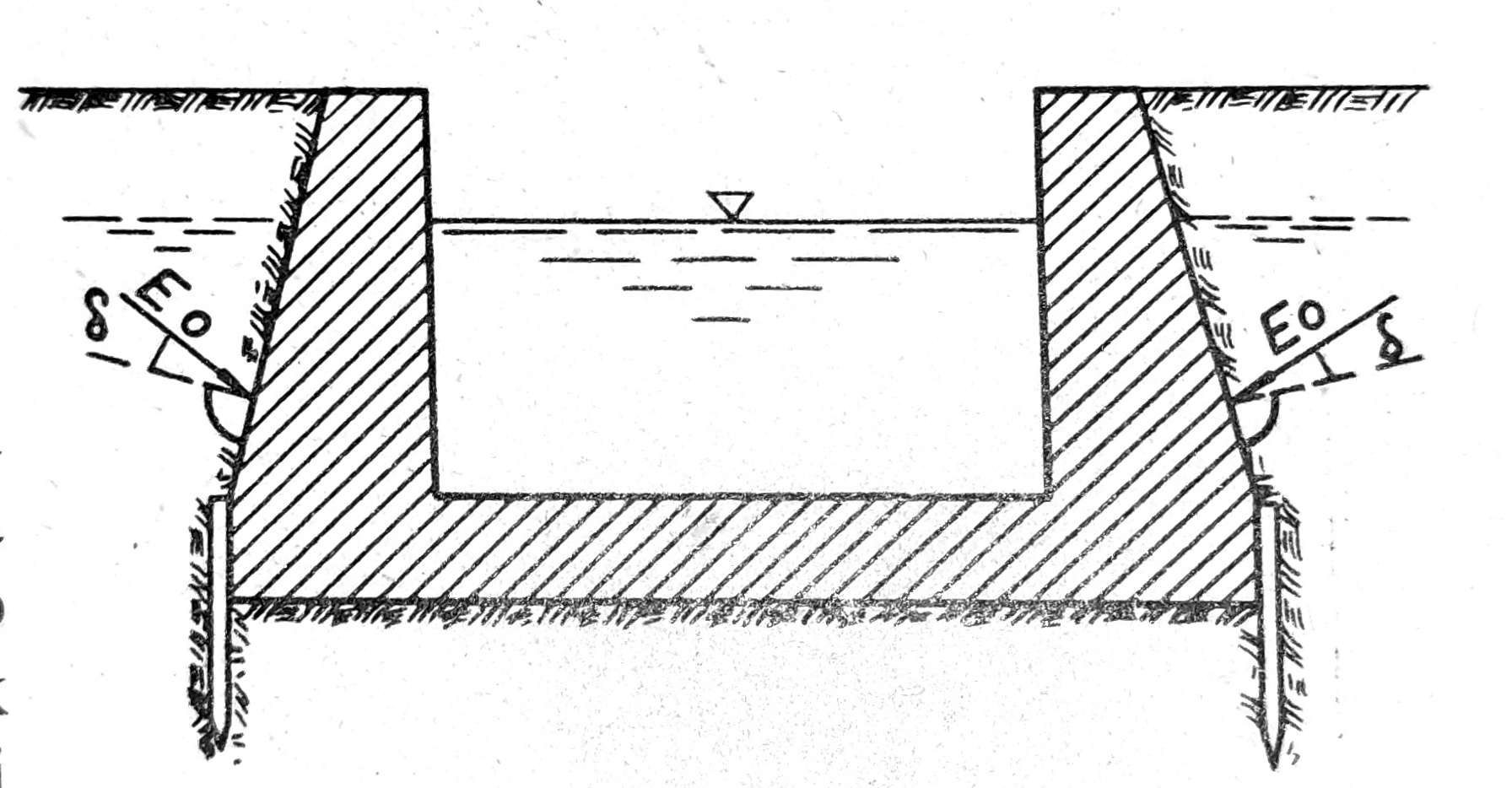
Sl. 2. Zemljani pritisak mirovanja na masivni dok
Ako se potporni zid pod dejstvom pritiska E pomera u napred ili obrće oko nožične tačke A, ili neke niže tačke, koji su slučajevi redovni u stišljivom tlu, sa izuzetkom napred navedenih zatvorenih i masivnih konstrukcija, tada se zemljana masa iza zida širi. Ako je pomeranje zida dovoljno veliko, otkida se jedan deo tla iza zida, prizma ABCA, i kliza naniže po kliznoj površini AC (sl. 2). Pritisak kojim klizajuća prizma deluje na potporni zid zove se aktivni zemljani pritisak i označuje se sa Ea. Ovaj pritisak je znatno manji od pritiska u stanju mirovanja, oko 0,5 do 0,7 E0. Usled klizanja zemljane prizme ABCA aktiviraju se duž obrazovane klizne površine AC naponi smicanja τ, koji se suprotstavljaju klizanju i smanjuju zemljani pritisak. U trenutku početka klizanja prizme ABCA naponi smicanja τ dostižu svoju najveću vrednost, što znači da je u tom trenutku vrednost aktivnog zemljanog pritiska E, najmanja. Prema tome, Ea je donja granična vrednost zemljanog pritiska.
Terzaghieva ispitivanja zemljanog pritiska sa peskovitim materijalom na zid visine h=1,50 m pokazala su, da je za dostizanje donje granične vrednosti aktivnog zemljanog pritiska Ea dovoljno srednje horizontalno pomeranje zida Δl od 5/10.000 visine zida ili obrtanje vrha zida Δl od 1/5.000 h oko nožice A.
Ako na zid delujemo pritiskom sa spoljne strane prema unutrašnjosti tla (sl. 3), zid će se pomerati unazad i tlo će se zbijati. Kada pomeranje zida dostigne izvesnu vrednost Δl, odvojiće se zemljana prizma ABCA od tla, koja će se pri daljem dejstvu spoljne sile istiskivati naviše po kliznoj površini AC. Otpor koji tlo pruži protivu dejstva spoljne sile u trenutku odvajanja prizme ABCA je pasivni zemljani, pritisak Ep. To je najveća gornja granična vrednost koju može dostići zemljani pritisak.
Zemljani pritisak u stanju mirovanja određuje se putem opita, dok se aktivni i pasivni zemljani pritisak mogu odrediti računskim putem, pomoću analitičkih ili grafičkih metoda, a na bazi poznavanja fizičkih karakteristika tla, obično određenih laboratorijskim putem.
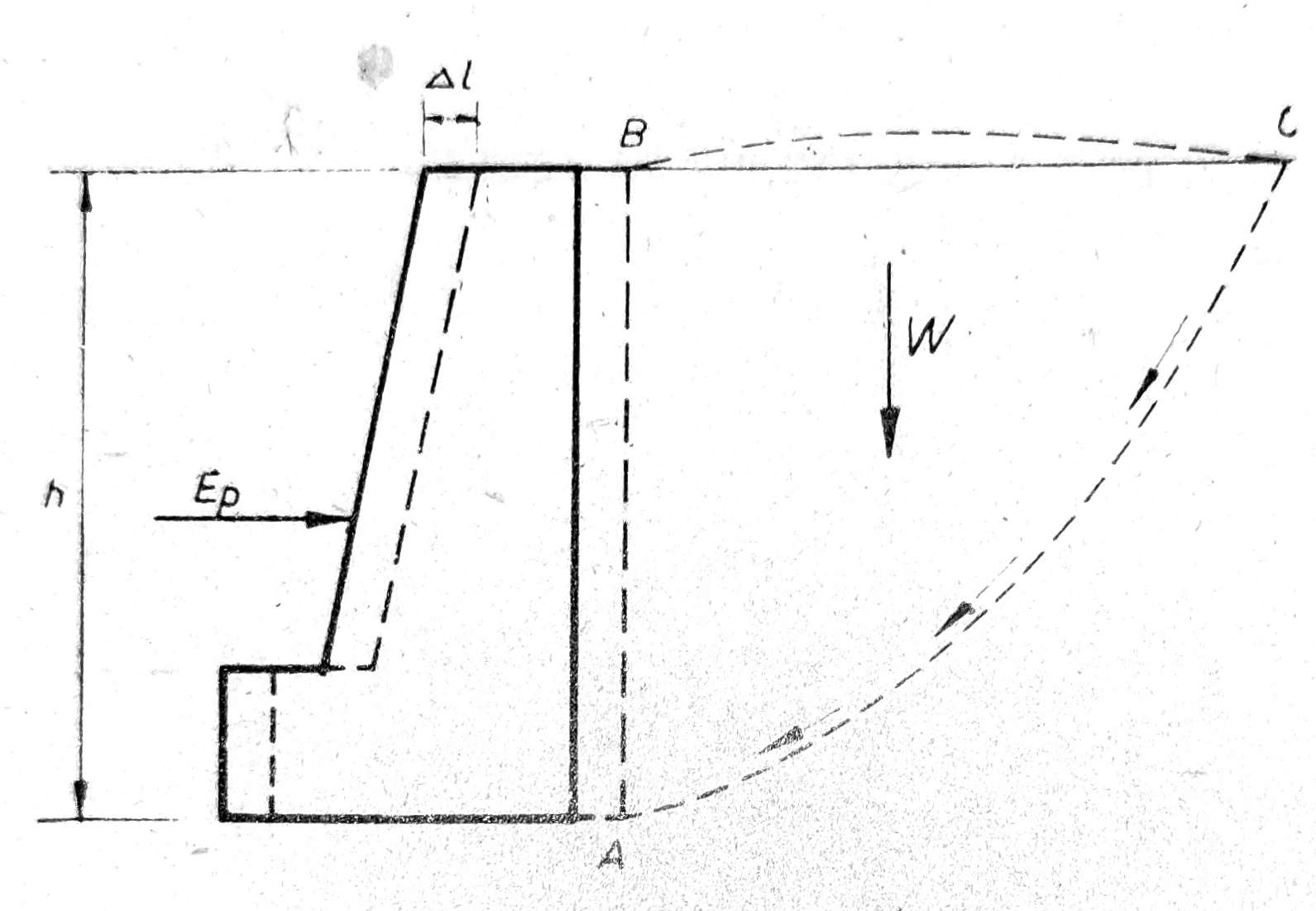
Sl. 3. Pasivni zemljani pritisak
Određivanje koeficijenta pritiska mirovanja K0
U slučaju kada je potporni zid izložen dejstvu pritiska mirovanja, za dimenzionisanje potpornog zida treba usvojiti pritisak mirovanja E0, koji je veći od aktivnog zemljanog pritiska. Njegova veličina nalazi se između aktivnog i pasivnog zemljanog pritiska, u zavisnosti od vrste tla i njegove zbijenosti.
Na dubini t ispod površine terena, vertikalni pritisak od sopstvene težine tla je σt = γ·t. Ako ne postoji mogućnost bočnog širenja tla, na dubini t deluje horizontalni pritisak σh = γ·t·K0, gde je K0 = σh/σt.
K0 je pritisak mirovanja. Koeficijent pritiska mirovanja može se odrediti triaksialnim opitom na sledeći način.
Uzorak neporemećenog tla izvađen sa dubine dejstva pritiska mirovanja stavi se u triaksialni aparat, gde se bočni pritisak σ3 pri primeni vertikalnog opterećenja σ1 podešava tako, da ne dođe do bočnih deformacija, tj. da bočna deformacija uzorka bude jednaka nuli. Vrednosti tako dobijenih efektivnih napona σ'1 i σ'3 nanose se na dijagram σ'1 – σ'3 (sl. 4), te se dobije prava linija tangentna na početni deo dijagrama, čiji nagib određuje vrednost K0 = σ'3/σ'1.
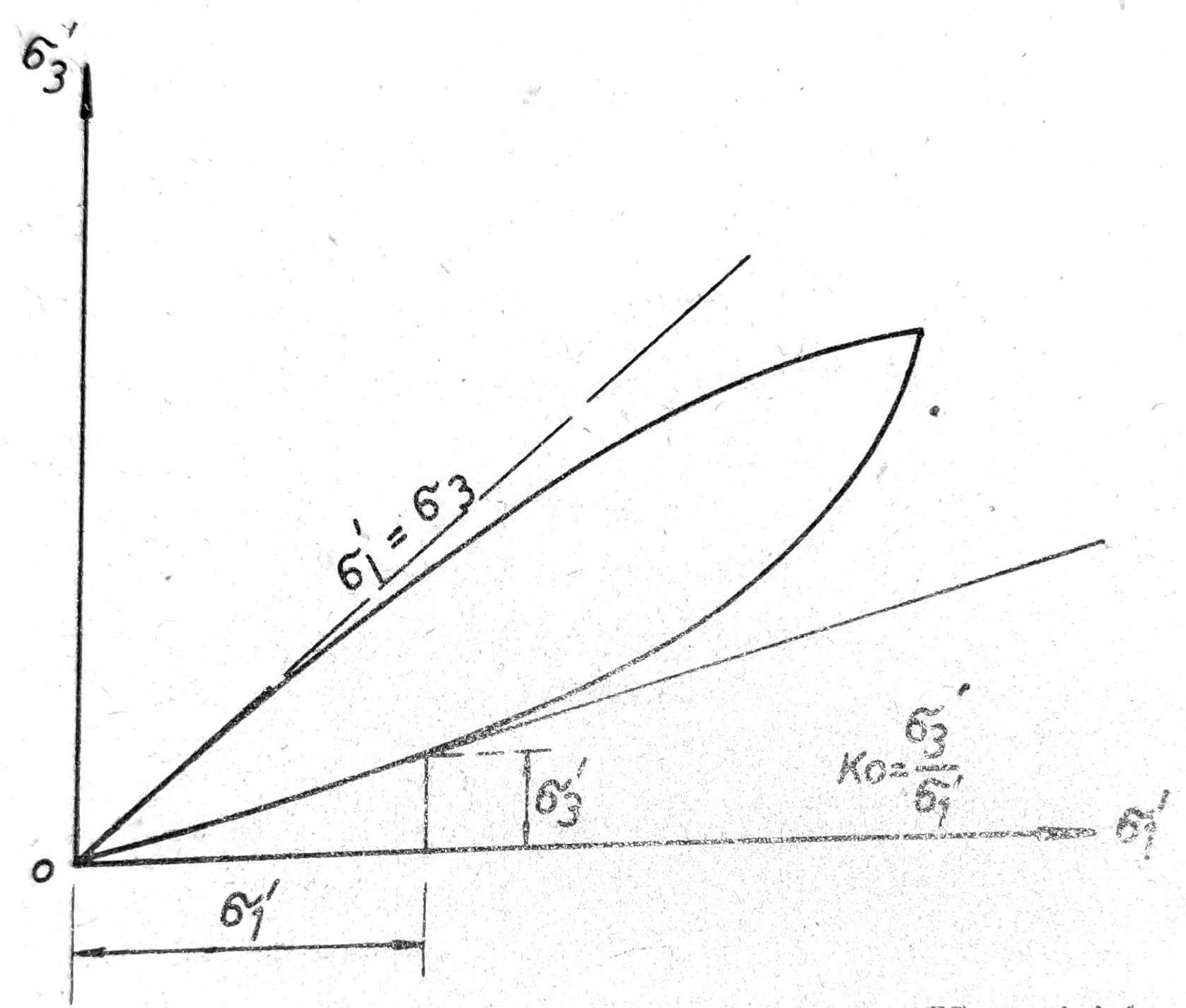
Sl. 4. Određivanje koeficijenta K0 pritiska mirovanja triaksijalnim opitom
Prema Petermannu, približne vrednosti koeficijenta pritiska mirovanja su
za zbijeni pesak K0 = 0,40 – 0,45
za rastresiti pesak K0 = 0,45 – 0,50
za glinu K0 = 0,60 – 0,75
Metode određivanja aktivnog zemljanog pritiska – Coulombova teorija zemljanog pritiska
Coulomb je prvi objavio teoriju zemljanog pritiska (1770. god.), zasnovanu na terenskom opitu. On je posmatrao potporni zid koji podupire nevezano tlo. U jednom trenutku uklonio je zid, pri čemu je zemljana masa skliznula po nekoj površini klizanja AC, nagnutoj pod uglom a sa horizontalom (sl. 5). Težina W klizajuće zemljane prizme ABC, ograničene površinom terena BC, kliznom površinom AC i potpornim zidom AB, deluje istovremeno na potporni zid i na kliznu površinu. Veličinu aktivnog zemljanog pritiska Ea, Coulomb je odredio pod sledećim dvema pretpostavkama:
1) da je površina klizanja prava površina;
2) da se tri delujuće sile: težina klizajuće prizme W, otpor potpornog zida Ea i otpor trenja Q duž klizne površine AC seku u jednoj tački što znači da se plan sila zatvara. Prema ovoj pretpostavci, u stanju granične ravnoteže težina W poništava se istovremeno otporom potpornog zida Ea i otporom trenja Q duž klizne površine.

Sl. 5. Određivanje aktivnog zemljanog pritiska po Columbovoj teoriji
Prednje pretpostavke ne odgovaraju stvarnosti. Klizna površina nije prava već kriva površina. Presecanje triju delujućih sila postoji samo u jednom slučaju, kada je površina terena iza zida horizontalna, unutrašnja površina zida vertikalna i pravac sile Ea horizontalan, dok u ostalim slučajevima ne postoji. Međutim i pored ovih odstupanja, određivanje aktivnog zemljanog pritiska još i danas se zasniva na Coulombovoj teoriji, pošto se pokazala praktično upotrebljiva u mnogim slučajevima.
Za određivanje aktivnog zemljanog pritiska Ea Coulomb je pretpostavio, da je usled dejstva težine zemljane mase W nastalo pomeranje potpornog zida i obrazovanje prizme ABC aktivnog zemljanog pritiska. Usvajajući da se unutrašnji otpor tla sastoji samo iz trenja. Coulomb razlaže težinu W u dve komponente, jednu u pravcu sile aktivnog zemljanog pritiska Ea, drugu u pravcu rezultante otpora trenja Q duž klizne površine (sl. 5b). Pri tome Coulomb dalje usvaja, da komponenta deluje pod uglom unutrašnjeg trenja sa normalom na kliznu površinu AC, a da komponenta Ea, deluje pod uglom odstupanja δ sa normalom na unutrašnju površinu zida AB. Sila W određena je po pravcu, veličini i smeru.
Za datu kliznu površinu pod uglom α sa horizontalom, sila W dobija se iz površine zemljane prizme ABC za dužinu 1,0 m upravnu na nacrt i zapreminske težine tla γ, W=AΔABC x 1,00 x γ. Sile Ea i Q poznate su po pravcima. Na osnovu plana sila (sl. 5b) i sinusne teoreme imamo:
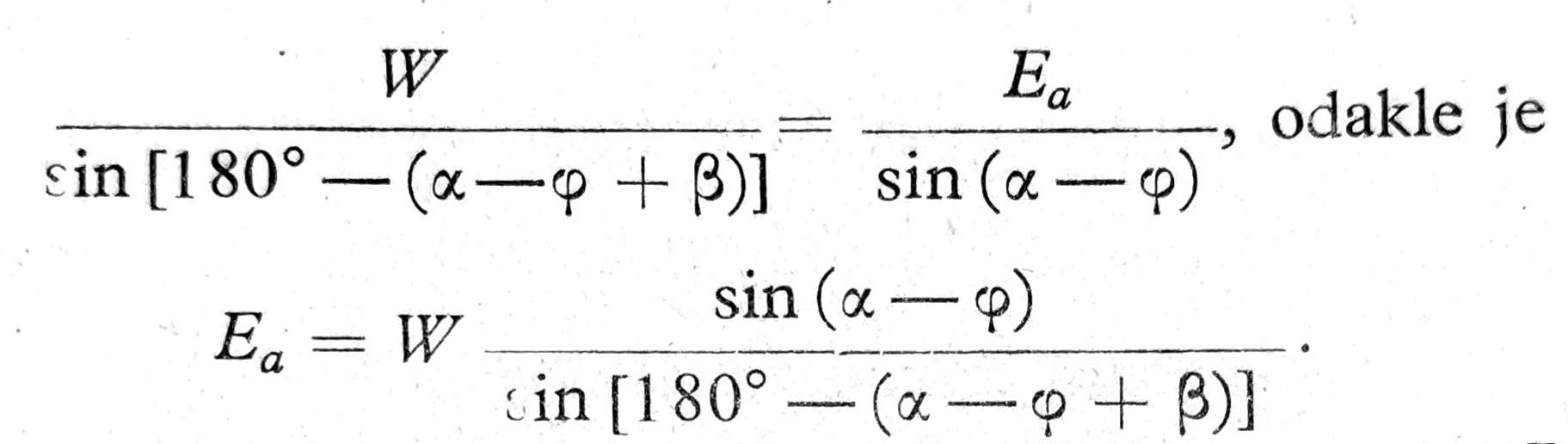
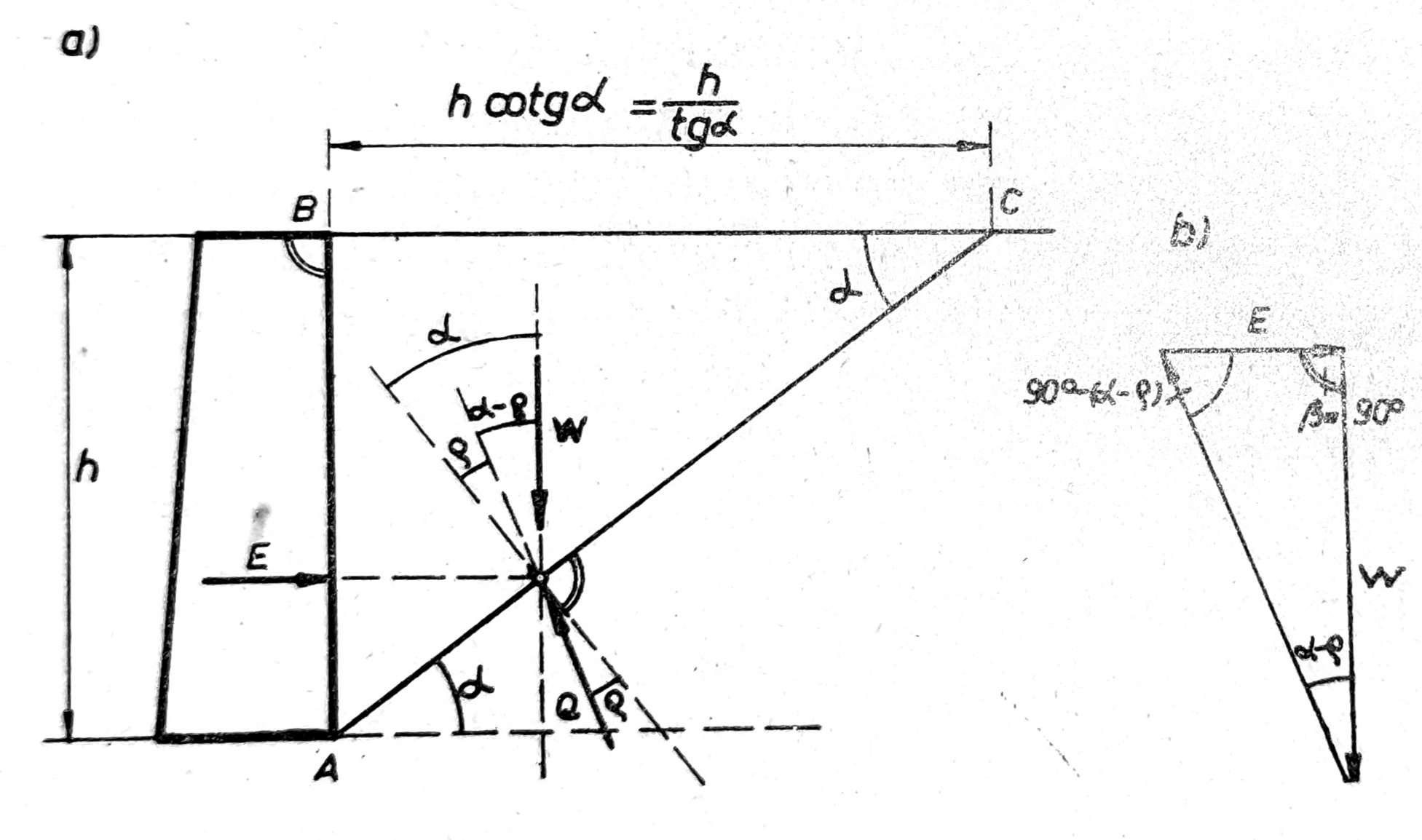
Sl. 6. Slučaj presecanja u jednoj tački delujućih sila kod potpornog zida
Ovaj obrazac tačan je samo u slučaju kada je teren horizontalan (v=0), unutrašnja površina zida vertikalna (θ=0) i pravac sile Ea horizontalan (δ=0) tj. kada je zid potpuno gladak (sl. 6).
Za ovaj specijalni tzv. Rankinov slučaj imamo:
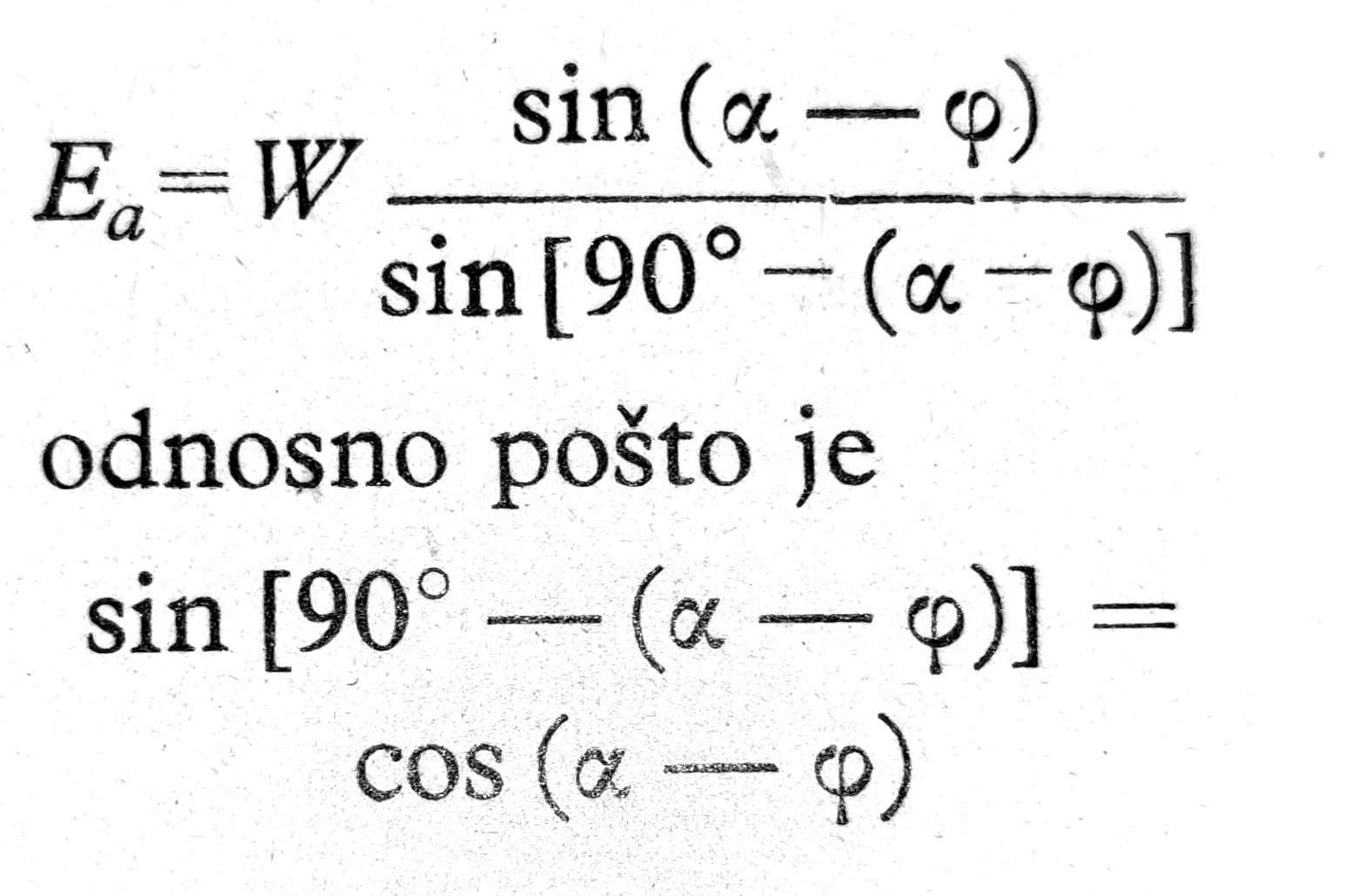
Težina W je u ovom slučaju W = 0.5·γ·h2/tgα, gde je γ zapreminska težina tla.
Ako prednju vrednost uvedemo u jednačinu za Ea, dobijamo:

Prednja jednačina odnosi se na proizvoljnu kliznu površinu AC. Međutim treba odrediti silu Ea za kritičnu kliznu površinu, tj. onu po kojoj će najverovatnije doći do klizanja. To će biti površina koja daje najveću vrednost aktivnog zemljanog pritiska max Ea.
Za datu visinu zida H i usvojeni stalni ugao unutrašnjeg trenja ϕ, vrednost aktivnog zemljanog pritiska varira sa uglom nagiba α klizne površine prema horizontali. Vrednost max Ea dobićemo ako diferenciramo Ea po α i stavimo da je diferencijal jednak nuli:

Određivanje uglova ϕ i δ
Ugao unutrašnjeg trenja ϕ određuje se laboratorijskim putem. Njegova veličina zavisi od vrste tla, stanja vlažnosti i zbijenosti. Za pojedine vrste tla, vrednost ugla ϕ kreće se najčešće u granicama datim u tablici 1.

Tabl. 1. Približne vrednosti ugla unutrašnjeg trenja ϕ za pojedine vrste tla
Ugao odstupanja δ sile Ea od normale na unutrašnju površinu zida zavisi od deformacije zida i tla iza njega i od rapavosti unutrašnje površine zida. Ako je sleganje tla veće od sleganja zida što je najčešći slučaj, onda je ugao δ pozitivan, trenje između zida i tla deluje naviše. Ako je sleganje zida veće od sleganja tla, što je izuzetan slučaj, onda je ugao δ negativan, trenje između zida i tla deluje naniže. Granične vrednosti ugla δ su za potpuno glatku površinu zida δ=0, za potpuno rapavu δ=ϕ. Uopšte se usvaja δ=2/3ϕ, s tim da je tlo zida trajno zaštićeno od jakog raskvašavanja. Ako je tlo iza zida izloženo jakim potresima, usvaja se δ=ϕ/2, a ako je jako raskvašeno δ=0.
Raspodela zemljanog pritiska iza zida i napadna tačka sile Ea

Sl. 7. Raspored zemljanog pritiska pri obrtanju potpornog zida oko nožžične tačke A
Raspodela zemljanog pritiska duž unutrašnje površine zida zavisi od deformacije potpornog zida, od oblika površine da iza zida i od oblika unutrašnje površine zida.
Napadna tačka aktivnog zemljanog pritiska Ea zavisi od raspodele pritiska duž unutrašnje površine zida i od njenog oblika. Ona je uvek u visini težišta površine dijagrama pritiska.
Coulomb je usvojio da zemljani pritisak iza zida linearno raste sa dubinom, kao kod vode, tzv. hidrostatičku raspodelu zemljanog pritiska (sl. 7). Međutim hidrostatička raspodela pritiska postoji samo u slučaju kada se zid obrće oko nožice A ili neke niže tačke, dok u svima drugim slučajevima odstupa od nje.
Ako se potporni zid obrće oko nožične tačke A, ili neke niže tačke, nastaje pokretanje tla naniže (sl. 7a), pri čemu ne dolazi do potiskivanja prema unutrašnjosti tla. U ovom slučaju pojavljuje se klizanje tla po površinama najmanjeg otpora M1C1, M2C2... paralelnih kliznoj površini AC, koja nastaje kada je obrtanje zida dovoljno veliko, da se obrazuje prizma klizanja ABCA.
Prema tome u ovom slučaju pritisak raste proporcionalno sa dubinom, tj. raspodela zemljanog pritiska je po Coulombu hidrostatička. Dijagram aktivnog zemljanog pritiska dobićemo na osnovu poznavanja sile Ea i visine zida h, pošto je sila Ea jednaka površini dijagrama pritiska abc (sl. 7b):
Ea=x·h/2, odakle je x=2Ea/h,
odnosno pošto je Ea = ½ γh2Ka, x = γhKa.

Sl. 8. Raspodela zemljanog pritiska pri obrtanju zida oko vrha B ili neke više tačke L
Ako se potporni zid obrće oko vrha zida B ili neke više tačke L (sl. 8a), dolazi do potiskivanja u gornjem delu prema unutrašnjošti tla, koje se usled toga istiskuje naviše po površinama najmanjeg otpora M1C1, M2C2... Pri dovoljno velikom obrtanju zida obrazuje se klizna površina AC, duž koje klizna prizma pri istiskivanju kliza naniže. Usled potiskivanja tla u gornjem delu pojavljuje se pasivni zemljani pritisak, koji je znatno veći od aktivnog, te u tom delu dijagram pritiska bd odgovara pasivnom pritisku Ep (sl. 8b). Kako ukupan zemljani pritisak Ea zavisi od veličine zemljane prizme ABCA i jednak je trougaonoj površini dijagrama pritiska abe, to će ovaj dijagram u svom daljem toku opadati, da bi se na kraju njegova površina izjednačila sa trougaonom površinom abe. Stvarni dijagram pritiska u ovom slučaju je krivolinijski bc, koji se matematičkim putem ne može odrediti. Međutim težište S površine dijagrama ac je iznad težišta površine trouglog dijagrama, što je nepovoljnije za stabilnost potpornog zida, jer je napadna tačka sile Ea viša. Prema Terzaghiu ona se nalazi na polovini visine potpornog zida.
Ako se potporni zid translatorno pomera unapred (sl. 9a), pritisak koji je pre pomeranja odgovarao zemljanom pritisku u stanju mirovanja E0 opada, pri čemu ne dolazi do pojave površina manjeg otpora, već se pri dovoljno velikom pomeranju zida stvara klizna površina AC, po kojoj zemljana prizma ABC kliza naniže. Pošto je ukupan pritisak jednak trougloj površini dijagrama pritiska abe (sl. 9b), to će dijagram pritiska u svom daljem toku opadati. Stvarni dijagram pritiska je kriva linija ac, koja se matematičkim putem ne može odrediti. Prema Terzaghiu, težište S je na visini 0,40 – 0,45h.
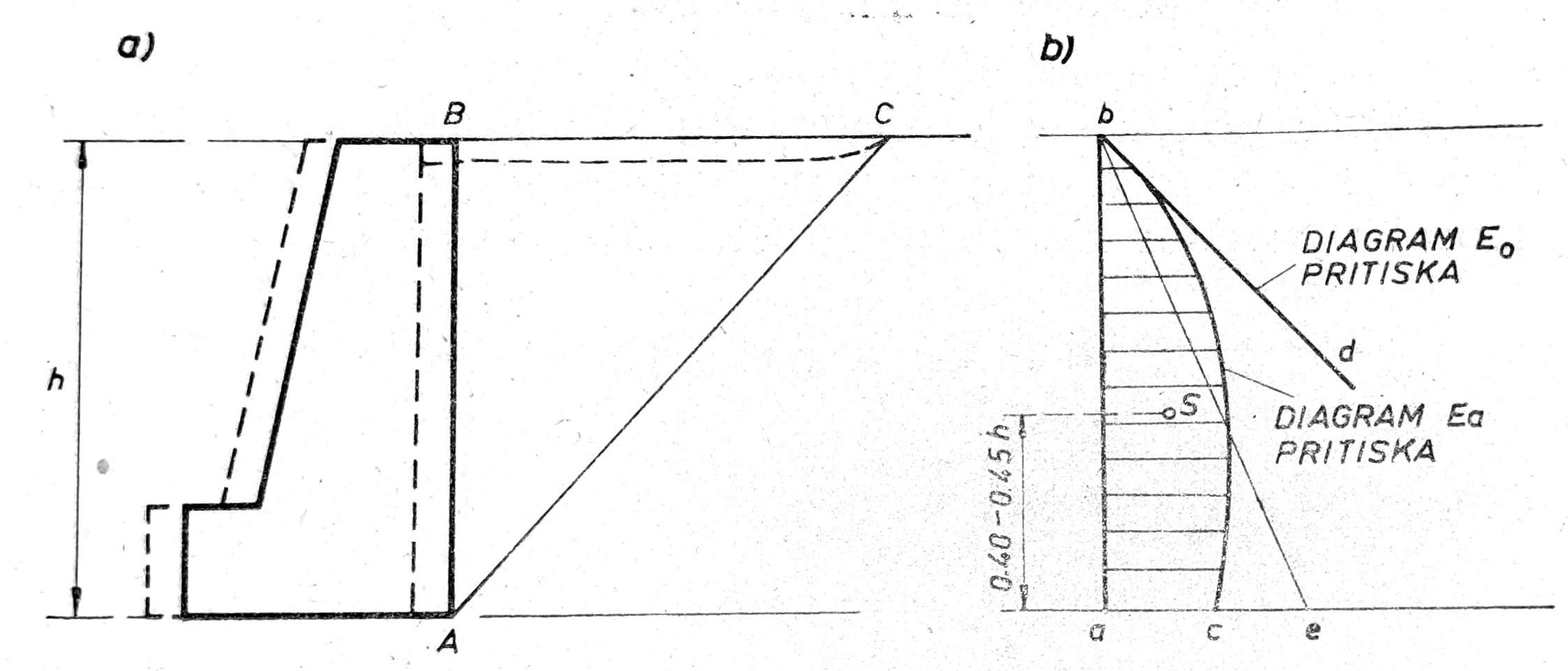
Sl. 9. Raspodela zemljanog pritiska pri translatornom pomeranju potpornog zida unapred
S obzirom na način određivanja zemljanog pritiska kao ekstremne vrednosti, najveće za aktivni a najmanje za pasivni, Columbova teorija se smatra kao ekstremna metoda određivanja zemljanog pritiska.
