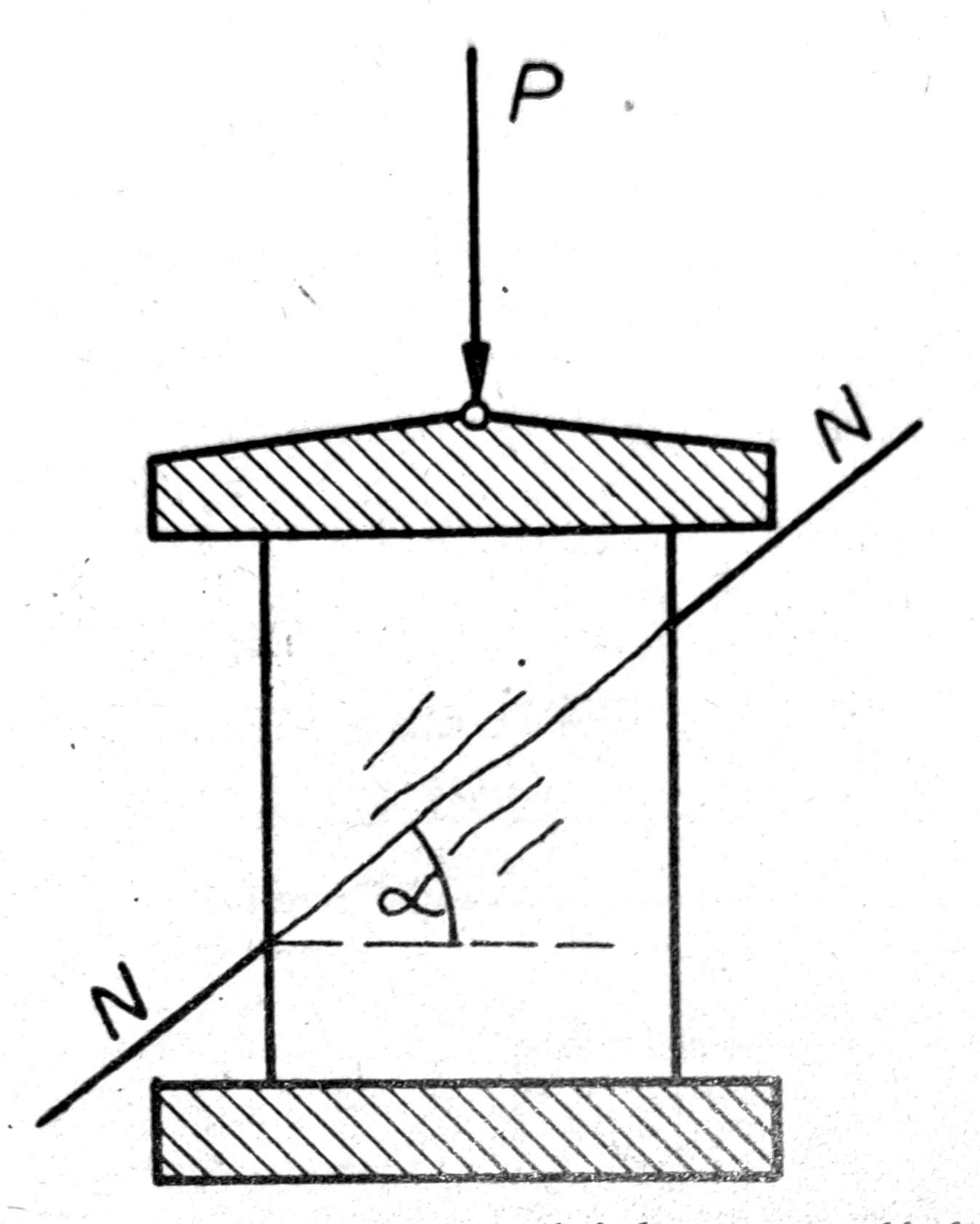
Ako u vezanom tlu isečemo valjak i stavimo ga pod dejstvo normalnog pritiska P (sl. 1), u valjku će se pojaviti novi naponi i to vertikalni napon pritiska σ i horizontalni napon smicanja . Ako pritisak P postupno povećavamo, posle izvesnog vremena pojaviće se na valjku kose pukotine, a odmah zatim nastaće lom valjka. U trenutku loma valjak je smaknut pod dejstvom pritiska P a po smičućoj ravni najmanjeg otpora N-N.
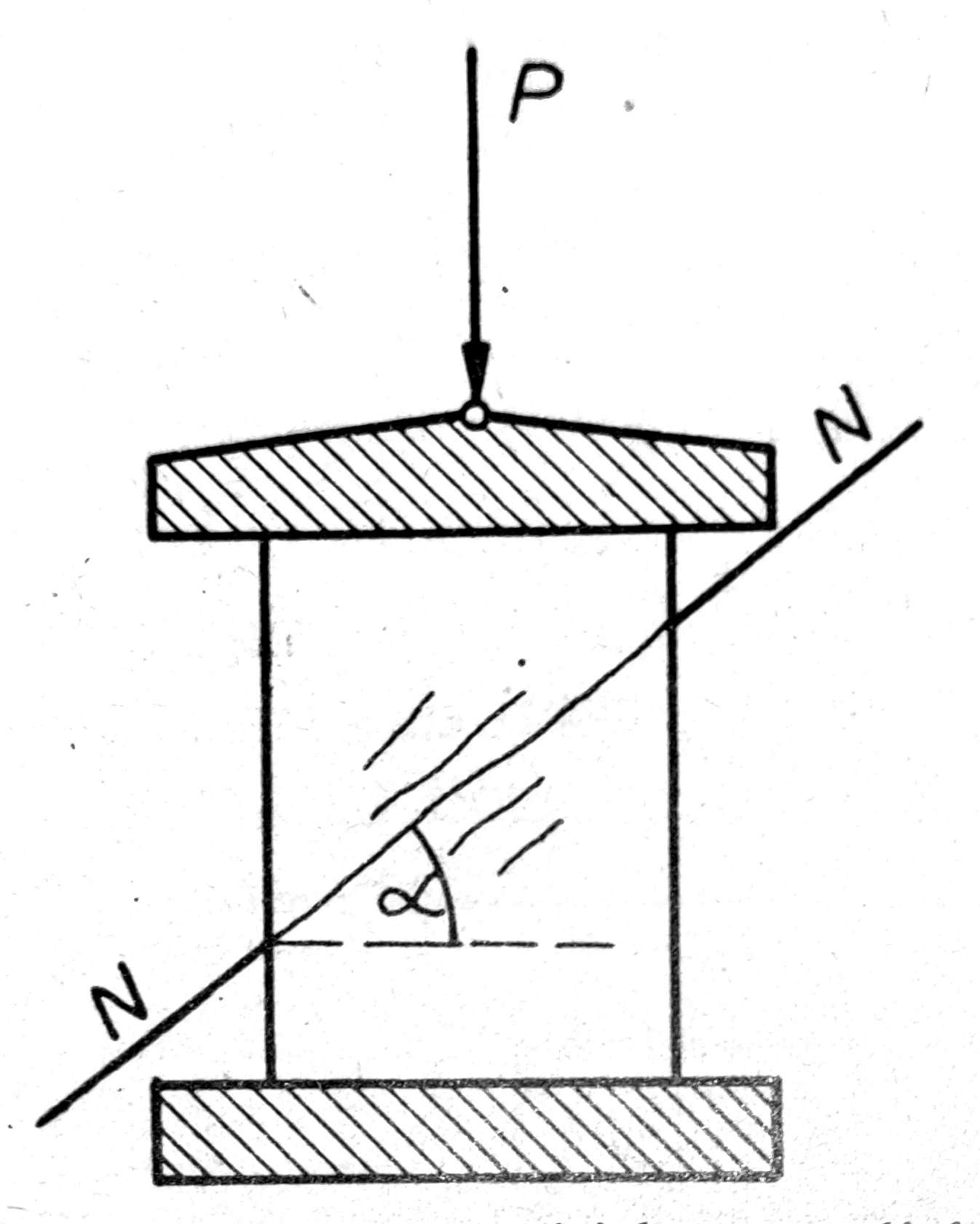
Sl. 1. Dejstvo pritiska na valjak izvađenog iz koherentnog tla
Otpor tla koji je valjak pružio protiv dejstva sile P u trenutku loma zove se otpor smicanja tla, a ugao α nagiba ravni najmanjeg otpora prema horizontali zove se ugao ravni najmanjeg otpora smicanja tla.
Otpor smicanja vezanog tla sastoji se iz dva elementarna otpora: unutrašnjeg trenja izmedu čvrstih čestica i kohezije koja vezuje čvrste čestice. Čvrstoća smicanja tla usvaja se da je jednaka najvećem naponu smicanja u trenutku loma i izražava se jednačinom
τf = c + σ tgφ
gde je: τf čvrstoća smicanja tla [kp/cm2],
c kohezija tla [kp/cm3],
σ normalni napon tla [kp/cm3],
φ ugao unutrašnjeg trenja tla.
Gornji obrazac dao je Francuz Coulomb 1785. god. Prema ovom obrascu, za dato tlo je kohezija c konstantna i nezavisna od normalnog pritiska, dok je otpor trenja σ tgϕ upravo proporcionalan sa naponom σ. U stavrnosti kohezija e nije konstantna za dato tlo, već je i ona u izvesnoj meri zavisna od normalnog napona σ, jer se pod dejstvom tog pritiska smanjuje debljina vodenog filma koji obavija čvrste čestice i time kohezija povećava. Coulombov obrazac važi za propustljiva tla, u kojima se pod dejstvom normalnog pritiska voda iz pora istiskuje bez otpora, što je slučaj šljunkovitog i peskovitog tla, ali nije slučaj vezanog tla, koje je malo propustljivo, zbog čega se voda iz pora teško istiskuje i zaostaje kao napregnuta porna voda pod dejstvom opterećenja P.
Efektivni i neutralni naponi u tlu
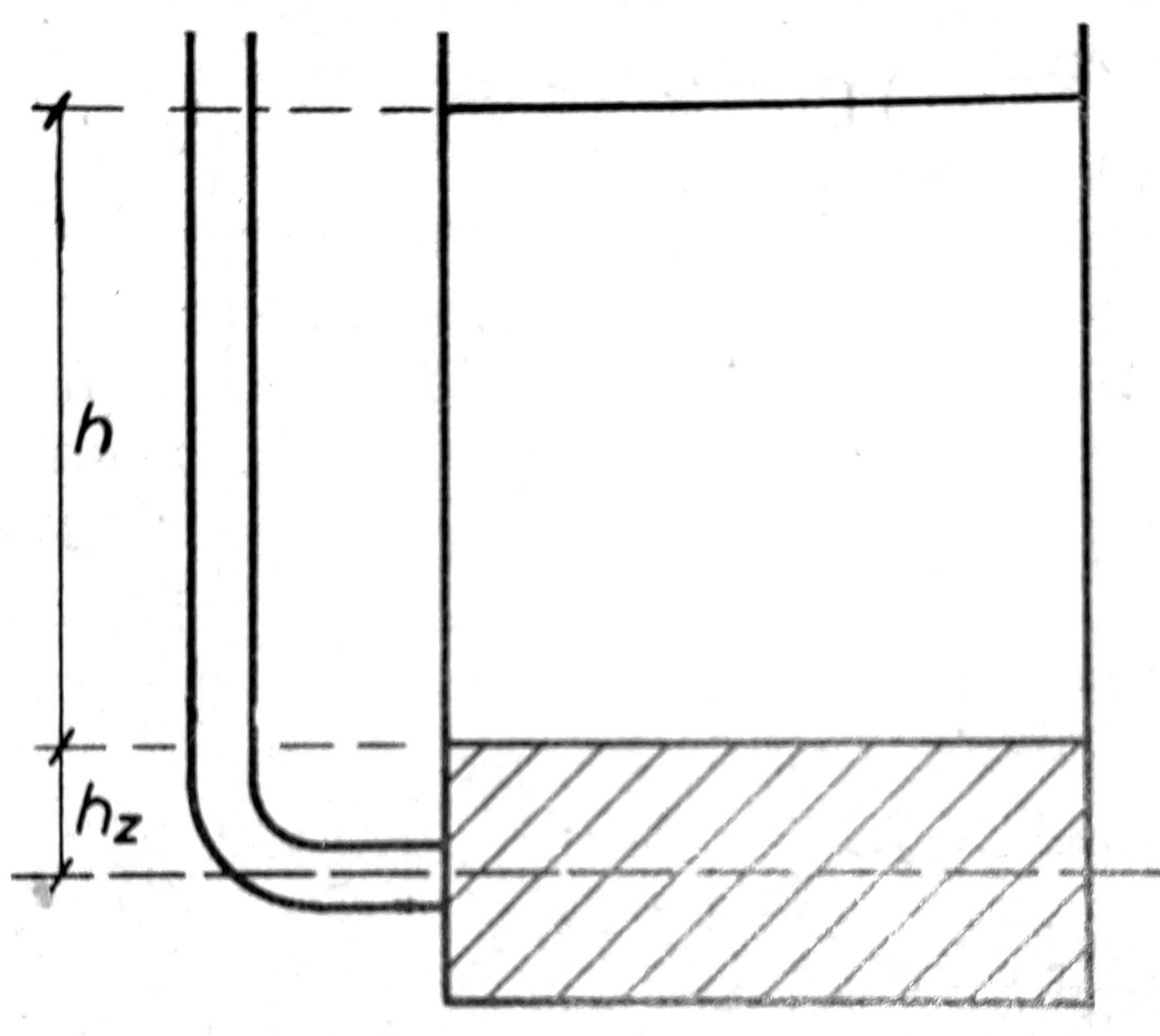
Sl. 2. Efektivni i neutralni napon u tlu
Ako na dno suda stavimo uzorak tla, na primer suvog peska, i opterećujemo ga nekom masom, na primer olovnom sačmom težine W, celokupno opterećenje ove težine primiće čvrste čestice tla. Specifični pritisak na površinu uzorka p0 = W/A u kp/cm3, gde je A površina preseka uzorka, izazvaće sleganje uzorka, tj. smanjenje njegove poroznosti, ali će takođe izazvati promene i drugih fizičkih osobina uzorka kao što su povećanje čvrstoće smicanja, povećanje modula stišljivosti i druge. Pritisak koji vlada na dodirnim površinama izmedu čestica zove se efektivni ili intergranularni pritisak σ'. Kada je postignuta konsolidacija tj. kada je uzorak prestao da se sleže pod opterećenjem p0, efektivni pritisak je jednak ukupnom specifičnom pritisku koji vlada na dubini u kojoj se tlo posmatra. U ovom slučaju je na dubini, ispod površine uzorka na sl. 2 σ’ = W/A + hzγ gde je γ zapreminska težina uzorka.
Medutim ako uzorak u sudu umesto olovnom sačmom opteretimo vodom do visine h, s tim da je ona ispunila sve pore uzorka, pritisak vodenog stuba iznad uzorka hγw, gde je γw zapreminska težina vode, neće prouzrokovati sleganje uzorka i smanjenje njegove poroznosti niti će povećati njegovu čvrstoću smicanja i modul stišljivosti. Zbog toga se hidrostatički pritisak hγw zove neutralni pritisak. Neutralni pritisak koji se označuje sa u prenosi se kroz uzorak u svima pravcima jednakim intenzitetom. Ovaj pritisak neće prouzrokovati povećanje čvrstoće smicanja, jer voda sama nema nikakvu čvrstoću smicanja.
Prema tome efektivni pritisak σ’ prenosi se preko dodirnih površina između čvrstih čestica tla, a neutralni pritisak u prenosi se kroz vodu u porama. Ako je donji deo suda ispunjen zasićenim uzorkom tla čija je zapreminska težina γz, a iznad površine uzorka do nivoa N je sud ispunjen vodom čija zapreminska težina je γw, onda će ukupan pritisak σ u ma kojoj tački uzorka biti σ = σ' + u.
Na dubini hz, ispod površine uzorka efektivni pritisak biće σ = σ' - u
gde je σ = h γw + h γz
u = (h + hz) γw.
Prema tome biće σ’ = hz γ’
γ’ je zapreminska težina potopljenog tla u vodu.
Opšta jednačina čvrstoće smicanja tla
Ako vezano tlo opteretimo opterećenjem P, ovo opterećenje izazvaće sleganje tla i najpre će pod njegovim dejstvom biti istisnut vazduh iz pora, tako da će uskoro u porama ostati samo voda. Pošto zbog male vodopropustljivosti vezanog tla voda ne može odmah da se istisne, to ona ostaje kao napregnuta voda u porama i u početku prima ukupno spoljno opterećenje P. U daljem vremenskom toku, pod dejstvom opterećenja P počinje da se istiskuje voda iz pora i nastaje zbližavanje čvrstih čestica, koje sada primaju jedan deo opterećenja P. Tada imamo τf =c + (σ - u) tgϕ, gde je σ ukupan pritisak od opterećenja P, u pritisak porne vode.
Pritisak porne vode u zavisi od više faktora, kao što su vremenski tok konsolidacije, propustljivost tla, veličina opterećenja tla itd. Čvrstoća smicanja tla zavisi od pritiska porne vode i ona je najveća za u=0, kada nastaje konsolidacija tla.
Koloidalna aktivnost tla
Elementi unutrašnjeg otpora tla kohezije i trenja mogu biti različiti i u velikoj meri zavise od krupnoće čvrstih čestica tla i njegovih plastičnih osobina. U cilju određivanja uticaja kohezije u odnosu na otpor unutrašnjeg trenja koherentnog tla, Skempton je uveo pojam koloidalne aktivnosti tla KP, koji je predstavljen odnosom indeksa plastičnosti IP prema količini čestica manjih od 0,002 mm u % težine cele mase. Pri tome je usvojen sledeći kriterijum (sl. 3):
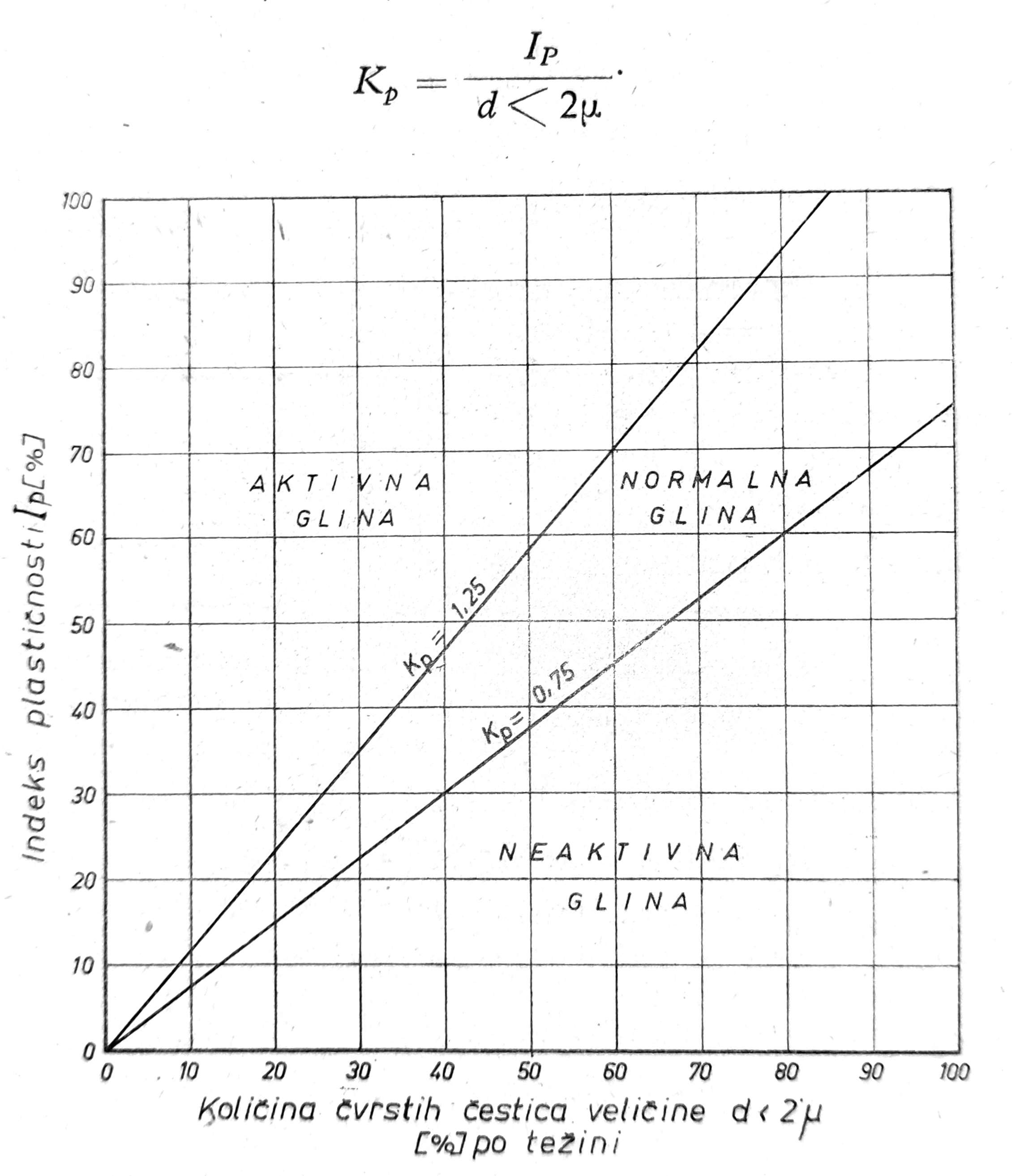
Sl. 3. Koloidalna aktivnost tla
Za KP < 0,75 su neaktivne gline,
za KP = 0,75 – 1,25 su normalne gline,
za Kp > 1,25 aktivne gline.
Sa povećanjem KP raste uticaj kohezije u odnosu na unutrašnje trenje koherentnog tla.
Osetljivost tla
Ako u koherentnom tlu izvadimo valjak prečnika 3—3,4 cm visine ~ 5 cm i opteretimo ga normalnim opterećenjem, u trenutku loma valjka dobićemo čvrstoću pritiska tla u neporemećenom stanju σₙ:
σn = P/A u kp/cm2,
gde je A poprečni presek valjka.
Po završenom opitu slomljeni uzorak premestimo i ponovo izradimo valjak istih dimenzija, pomoću istog cilindra-kalupa, s tim da njegova vlažnost ostane ona koja je bila pri prethodnom opitu. Zatim se odmah po izradi premešenog valjka ponovi opit sa njime, tako da se dobije čvrstoća pritiska tla u poremećenom stanju σₚ.
Osetljivost (sensitivitet) Sₜ je odnos čvrstoće pritiska u neporemećenom prema čvrstoći pritiska u poremećenom stanju: St = σn/σp,
Prema jednom kriterijumu osetljivost Sₜ ocenjuje se na sledeći način:
- za Sₜ = 1 — 2 je mala osetljivost gline,
- za Sₜ = 2 — 4 je srednja osetljivost gline,
- za Sₜ = 4 — 8 je velika osetljivost gline,
- za Sₜ > 8 je preosetljiva glina.
U prirodi se dešava da usled mehaničkog dejstva, na primer potresa, glinovito tlo odjednom izgubi svoju čvrstoću, koju zatim u stanju mirovanja ponovo dobije. Ova osobina zove se tiksotropija tla. Mnoge gline imaju u izvesnoj meri tiksotropne osobine. Poznati su slučajevi klizanja kosina useka usled isticanja tiksotropne gline u Norveškoj, Švedskoj i Finskoj, gde je ispitivanjem utvrđeno da nije bilo promene vlažnosti gline u toku ovog procesa, tj. da je vlažnost gline bila konstantna pre i posle isticanja.