Stišljivost tla određuje se opitom kompresije sa sprečenim bočnim širenjem koji se još zove edometarski opit ili opit konsolidacije.
Opit se vrši sa neporemećenim uzorcima, a u izvesnim slučajevima i sa poremećenim. U prvom slučaju, uzorak za vršenje opita uzima se utiskivanjem metalnih prstena u veći neporemećeni uzorak, koji se zatim po sasecanju viška uzorka i izravnavanju njegovih površina sa ivicama cilindra unosi u aparat zajedno sa prstenom. U drugom slučaju prsten se ispunjava uzorkom u stanju konsistencije na granici tečenja i u tom stanju se unosi u edometar.
Opit se vrši pomoću aparata koji je prvi konstruisao Terzaghi i nazvao ga edometar (Oedometer). Danas postoji više različitih konstrukcija ovog aparata, ali su svi oni zasnovani na istom principu, ispitivanju kompresije uzorka tla pod opterećenjem pri sprečenom bočnom širenju.
Opis aparata
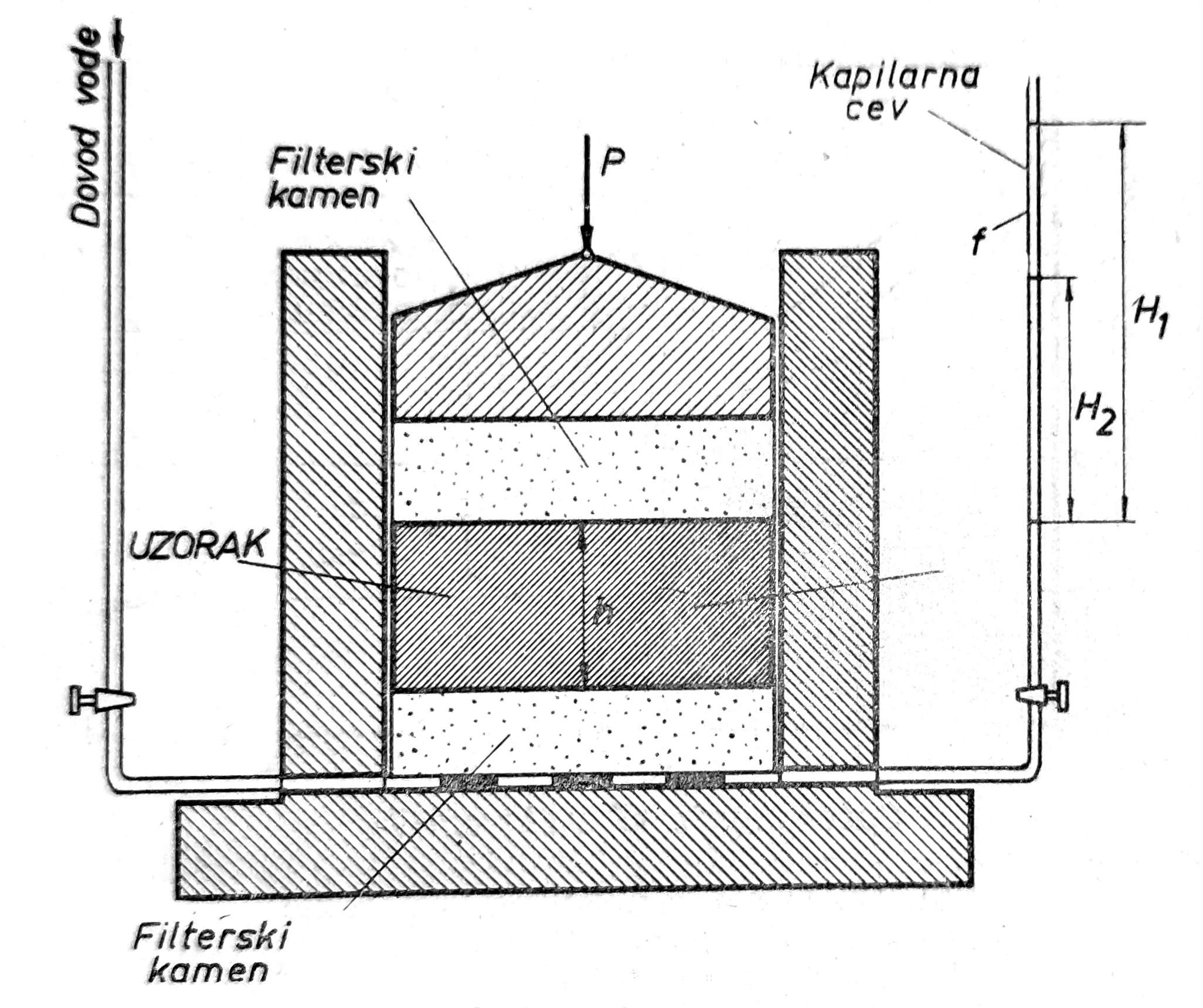
Sl. 1. Edometar
Edometar se sastoji iz metalnog cilindra u kome se uzorak nalazi izmedu dva filterska kamena (sl. 1). Uzorak se unosi u aparat u metalnom prstenu prečnika 7-10 cm, visine 1-4 cm. Preko gornjeg filterskog kamena prenosi se opterećenje P na uzorak. Ispod donjeg filterskog kamena nalaze se u dnu cilindra kanali za oticanje vode iz uzorka u kapilarnu cev, kao i za dovod vode. Pošto se kompresija uzorka vrši na račun pora, jer su čvrste čestice tla i voda u porama praktično nestišljivi, to je potrebno za vreme vršenja opita obezbediti oticanje vode iz uzorka, što je omogućeno pomoću filterskog kamena, kanala i kapilarne cevi.
Sa leve strane aparata je cev za dovod vode sa slavinom ispred cilindra, dok je kapilarna cev sa desne strane, sa slavinom iza cilindra. Kapilarna cev služi još i za određivanje koeficijenta propustljivosti tla k.
Vršenje opita
Kada je uzorak stavljen u cilindar i aparat sklopljen, zatvori se leva slavina, dovod vode, a otvori desna, za isticanje vode u kapilarnu cev. Potom se pristupa opterećenju uzorka, koje se nanosi postupno. Obično se nanose sledeća opterećenja: 0,50; 1,00; 2,00; 4,00; 6,00 kp/cm2 i dalje do najvećeg opterećenja tla koje se očekuje pod objektom, uglavnom do 10 kp/cm2, a kod brana može biti i više do 20 kp/cm2. Kod svakog stupnja opterećenja, u trenutku njegovog nanošenja pušta se u rad stoper časovnik i u određenim vremenskim razmacima 15", 30", 1', 2', 5', 15', 45', 2h, 5h, 24h, zatim svakih daljih 24h, sve do konsolidacije uzorka pod tim stupnjem opterećenja, čita se na komparateru odgovarajuće sleganje u hiljaditim delovima milimetra i beleži u zapisnik. Za konsolidaciju se usvaja da je ona postignuta ako je sleganje uzorka Δh ≤ 0,02 mm za vreme od 24 časa. Po postignutoj konsolidaciji, nanosi se sledeći stupanj opterećenja i ceo postupak se ponavlja na isti način te tako redom sve do krajnjeg stupnja opterećenja.
Opit konsolidacije sa sprečenim bočnim širenjem vrši se sa opterećenjem i rasterećenjem, da bi se utvrdile i elastične osobine tla. Pošto smo opteretili uzorak do izvesnog stepena, rasterećujemo ga sa istom postupnošću kao što smo ga opterećivali. Rasterećenje se vrši obično posle 2,0 kp/cm2, 4,0 kp/cm2 i 6,0 kp/cm2.
Po pravilu opit se vrši sa uzorkom pod vodom, koja se održava na levoj staklenoj cevi u visini gornje površine uzorka u aparatu. Ispitivanje stišljivosti uzorka u prisustvu vode vrši se zbog toga, jer opit traje dosta dugo i uzorak se za to vreme suši, usled čega bi se dobila manja stišljivost uzorka od stvarne stišljivosti tla u stanju njegove prirodne vlažnosti. Osim toga, prirodna vlažnost tla može biti veća nego što je bila pri vađenju uzorka, naročito pri izdizanju nivoa podzemne vode, što bi moglo dovesti do znatnog odstupanja od stvarne stišljivosti tla u vremenskom periodu visokog vodostaja.
Rezultati opita nanose se na tri vrste dijagrama i to dijagram relativne kompresije, dijagram promene koeficijenta poroznosti i dijagram vremenskog sleganja.
Dijagram relativne kompresije
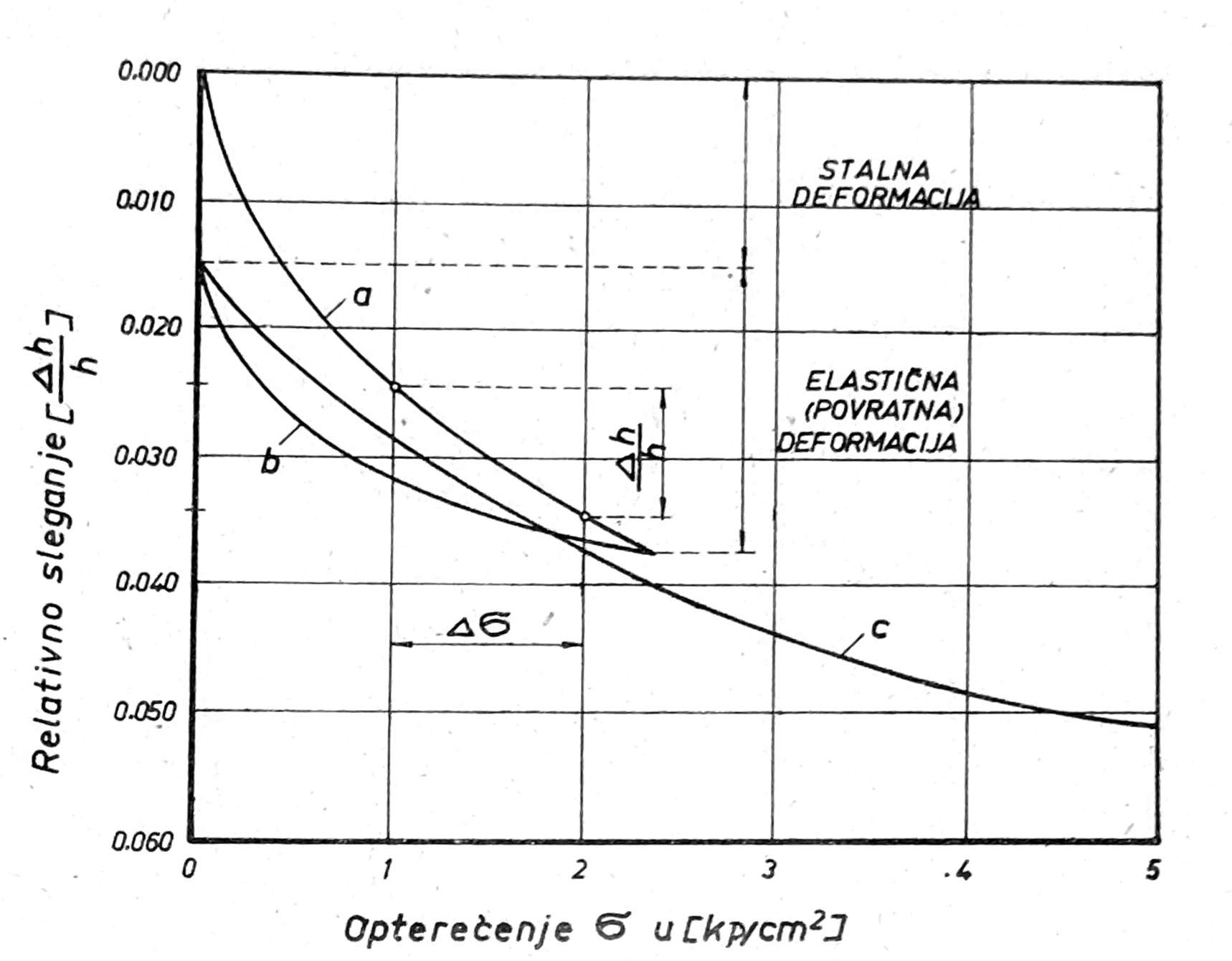
Ovaj dijagram se dobija kada se na osovinu apscisa nanese normalni pritisak na uzorak σ = P/A, gde je P opterećenje koje preko gornjeg filterskog kamena deluje na uzorak u kp/cm2, A površina poprečnog preseka uzorka u aparatu, a na osovinu ordinata relativna kompresija Δh/h gde je Δh sleganje uzorka pod opterećenjem Δσ pri konsolidaciji, h visina uzorka pre opterećenja (sl. 2).
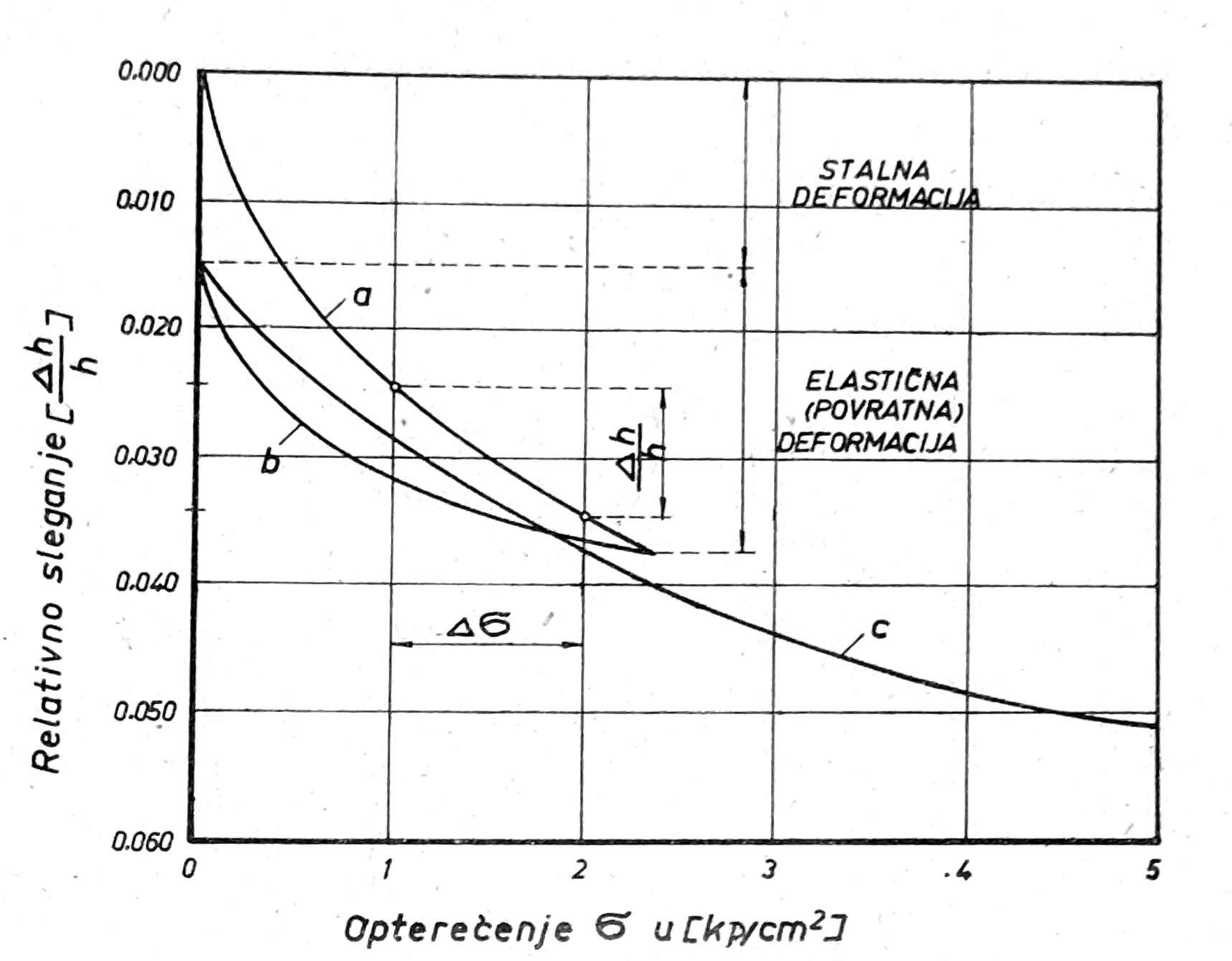
Sl. 2. Dijagram relativne kompresije
Pri opterećenju dobija se dijagram primarne kompresije a.
Pri rasterećenju, ako je omogućen nesmetani prijem vode, tako da je uzorak i za vreme rasterećenja ostao pod vodom on se vraća u prvobitno stanje, tj. bubri. Ipak uzorak se ne vraća u početno stanje, što znači da je pored elastične pretrpeo i plastičnu (stalnu) deformaciju. Prema tome u ovom slučaju, pri rasterećenju dobija se dijagram bubrenja b. Međutim ako je ispitivanje vršeno bez prijema vode, umesto dijagrama bubrenja dobija se tzv. dijagram elastičnosti.
Ukoliko se po rasterećenju vrši ponovo opterećenje uzorka, dobija se dijagram sekundarne kompresije c. Dijagram bubrenja bi dijagram sekundarne kompresije c obrazuju između sebe histerezisovu petlju. Kod gline su histerezisove petlje znatne i zbog toga se deformacija u oblasti bubrenja i sekundarne kompresije (dijagrami b i c) ne smatraju elastičnim, već povratnim (reversibilnim), pošto nisu proporcionalne opterećenju po Hookeovom zakonu. Deformacije u oblasti primarne kompresije (dijagram a) na delu gde se nisu vratile su stalne (ireversibilne).
Iz dijagrama relativne kompresije dobijamo po Hooke-ovom zakonu analogno Jungovom modulu elastičnosti E za elastičan materijal, modul stišljivosti tla Ms
Ms = Δσ / (Δh/h) [kp/cm2],
gde je Δσ priraštaj opterećenja, Δh/h odgovarajuća relativna kompresija, koja se uzima iz dijagrama primarne kompresije a (sl. 2).
Modul stišljivosti tla Ms, razlikuje se od modula elastičnosti E elastičnog materijala, jer Ms nije konstantan za jedan isti materijal već je promenljiv i raste sa normalnim opterećenjem σ. Prema tome, jedna određena vrednost modula stišljivosti Ms može se dati samo za jedan uski interval normalnog opterećenja tla Δσ. Ukoliko je vrednost modula Ms veća, utoliko je stišljivost tla manja i obratno. Po našim propisima za fundiranje, usvojen je sledeći kriterijum za modul stišljivosti tla u prirodnom stanju:
Ms = 0 - 20 kp/cm2 vanredno stišljivo tlo
Ms = 20 - 50 kp/cm2 vrlo stišljivo tlo
Ms = 50 - 100 kp/cm2 srednje stišljivo tlo
Ms = 100 - 400 kp/cm2 manje stišljivo tlo
Ms = 100 - 400 kp/cm2 malo stišljivo tlo
Ms = 400 - 1000 kp/cm2 malo stišljivo tlo
Ms > 1000 kp/cm2 vrlo malol stišljivo tlo.
Na isti način dobijamo modul elastičnosti tla E:
E = Δσ / (Δh/h) [kp/cm2],
gde se priraštaj relativne kompresije Δh/h uzima iz dijagrama elastičnosti tla za odgovarajući priraštaj normalnog pritiska Δσ.
Normalno konsolidovano i prekonsolidovano tlo
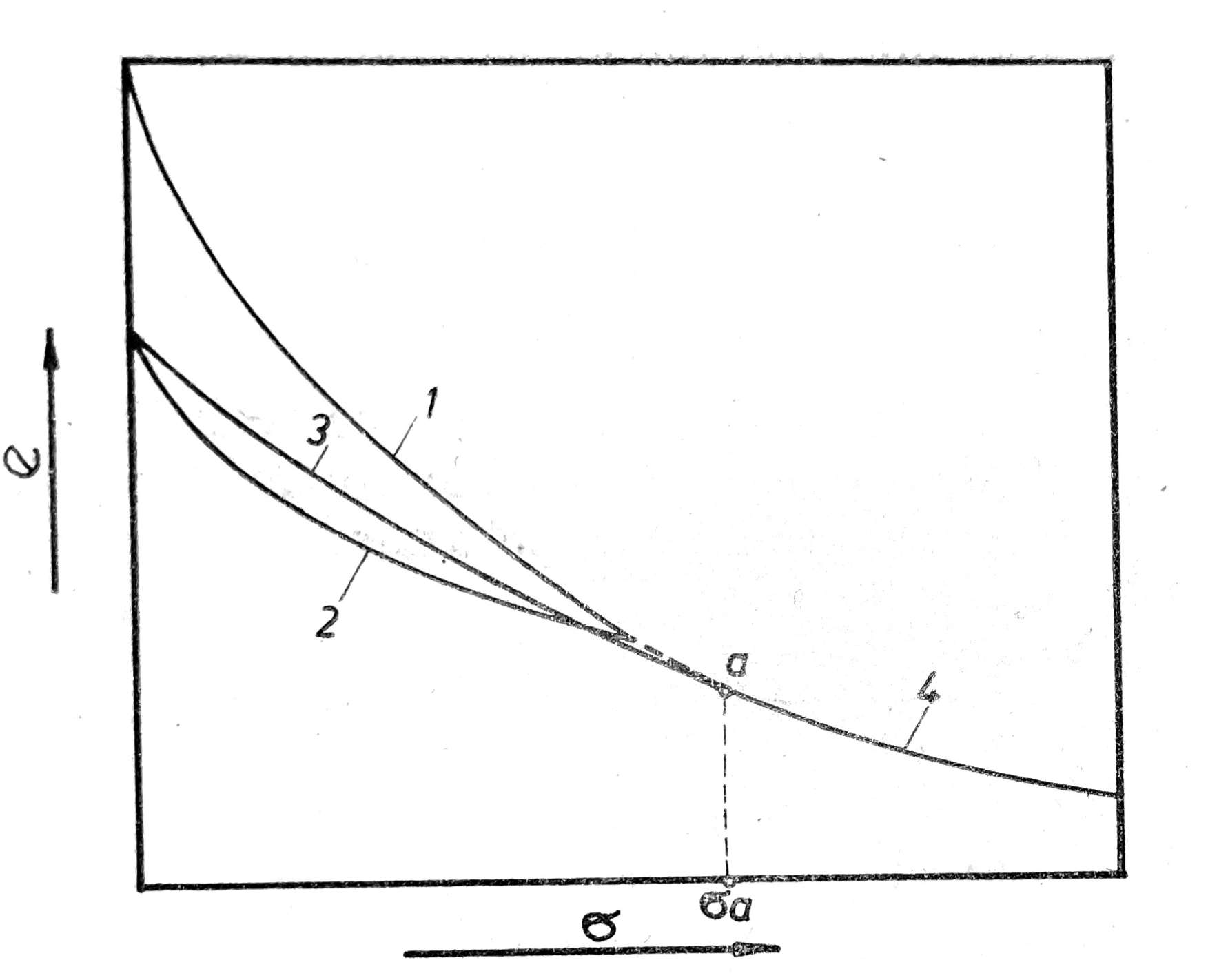
Sl. 3. Dijagram promene koeficijenta poroznosti uzorka poremećenog tla
Ako izvršimo edometarski opit sa poremećenim uzorkom, koga smo uneli u aparat na granici tečenja, i rezultate opita nanesemo na dijagram promene koeficijenta poroznosti e u zavisnosti od pritiska σ (sl. 3) tok konsolidacije predstavljen je dijagramima 1 za primarno opterećenje, 2 za rasterećenje, 3 za sekundarno opterećenje do granice a primarnog produžetka opterećenja σa i 4 izvan te granice.
Dijagram rasterećenja 2 i dijagram sekundarne kompresije 3 obrazuju histerezisovu petlju iza koje se dijagram 4 nastavlja u produženju dijagrama 1, bez preloma, kao da nije bilo rasterećenja i ponovnog opterećenja.
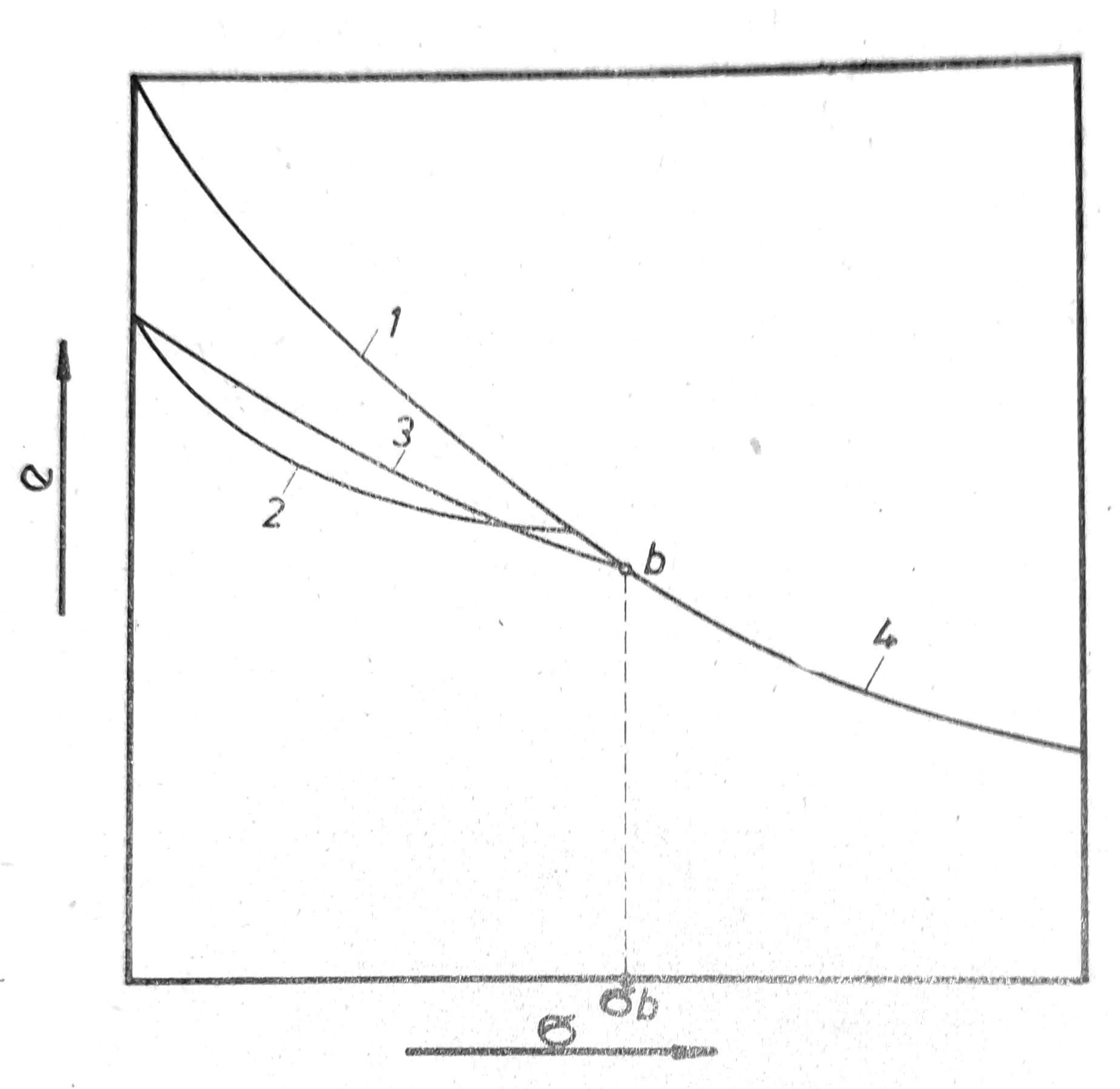
Sl. 4. Dijagram promene koeficijenta poroznosti uzorka neporemećenog tla
Međutim ako edometarski opit izvršimo na isti način kao napred sa neporemećenim uzorkom izvađenim sa izvesne dubine tla (sl. 4), dijagram za sekundarno opterećenje 3 pokazaće pri jednom određenom opterećenju σb prelom u tački b, posle koga će u daljem nastavku dijagram 4 imati veći nagib. Ovaj prelom nastao je zbog toga, jer je tlo iz koga je uzorak izvađen bilo pod većim opterećenjem p=γt, nego što je opterećenje uzorka σ u edometru. Veće opterećenje p potiče od težine postojećih gornjih slojeva tla do površine terena, koju nazivamo pritisak tla ili pak od opterećenja ranijih slojeva tla odnesenih tokom vremena erozijom ili odnesenog morenskog tla ili leda, koje nazivamo predopterećenje. Pojava prekonsolidacije naročito je karakteristična kod glina, gde razlikujemo normalno konsolidovanu i prekonsolidovanu glinu.
Normalno konsolidovana glina je na manjim dubinama ispod površine terena, koja nije bila ranije izložena predopterećenju. Uzorak ove gline, opterećen u edometru većim opterećenjima od težine gornjih slojeva „pritiska tla“ pokazuje kontinualan tok konsolidacije, bez preloma na dijagramu relativne kompresije ili na dijagramu promene koeficijenta poroznosti. Sleganje ove gline pod opterećenjem objekta je normalno, tj. pod određenim opterećenjem sleganje se tokom vremena smanjuje.
Prekonsolidovana glina je na većim dubinama ili je ranije bila izložena predopterećenju. Uzorak ove gline opterećen u edometru većim pritiskom od pritiska tla ili od predopterećenja pokazuje na dijagramu relativne kompresije ili na dijagramu promene koeficijenta poroznosti prelom, tzv. geološki prelom g, sa jakom promenom pravca (sl. 5a). Sleganje ove gline pod objektom je malo za opterećenje ispod pritiska tla ili predopterećenje σ1, ali postaje znatno veće za opterećenja iznad σ1.
Ako geološki prelom nije jasno izražen, onda se on određuje pomoću tangenata na dijagram (sl. 5b).
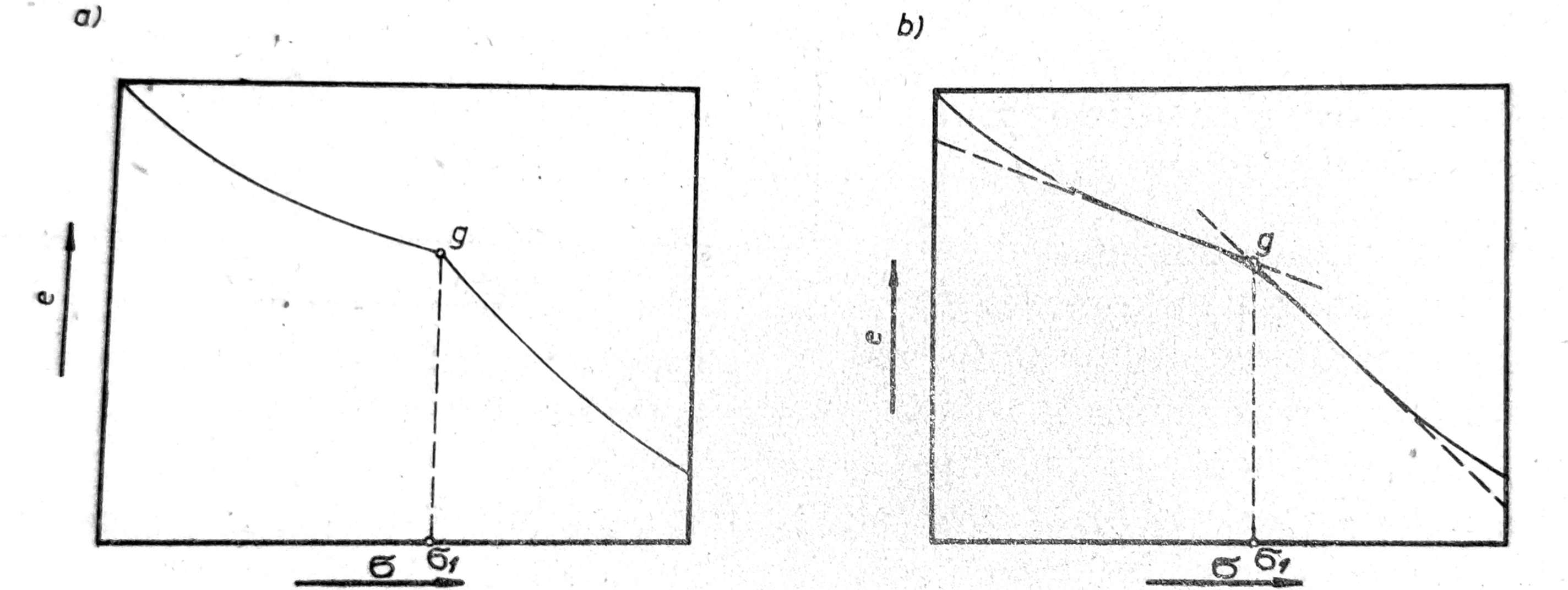
Sl. 5. Dijagram promene koeficijenta poroznosti prekonsolidovane gline
Dijagram vremenskog sleganja
Ovaj dijagram, nazvan još dijagram konsolidacije, dobija se kada se za svaki stupanj opterećenja uzorka u edometru nanese na osovinu apscisa vreme t u časovima, a na osovinu ordinata sleganje u mm (sl. 6a) ili u % od ukupnog sleganja (sl. 6b).
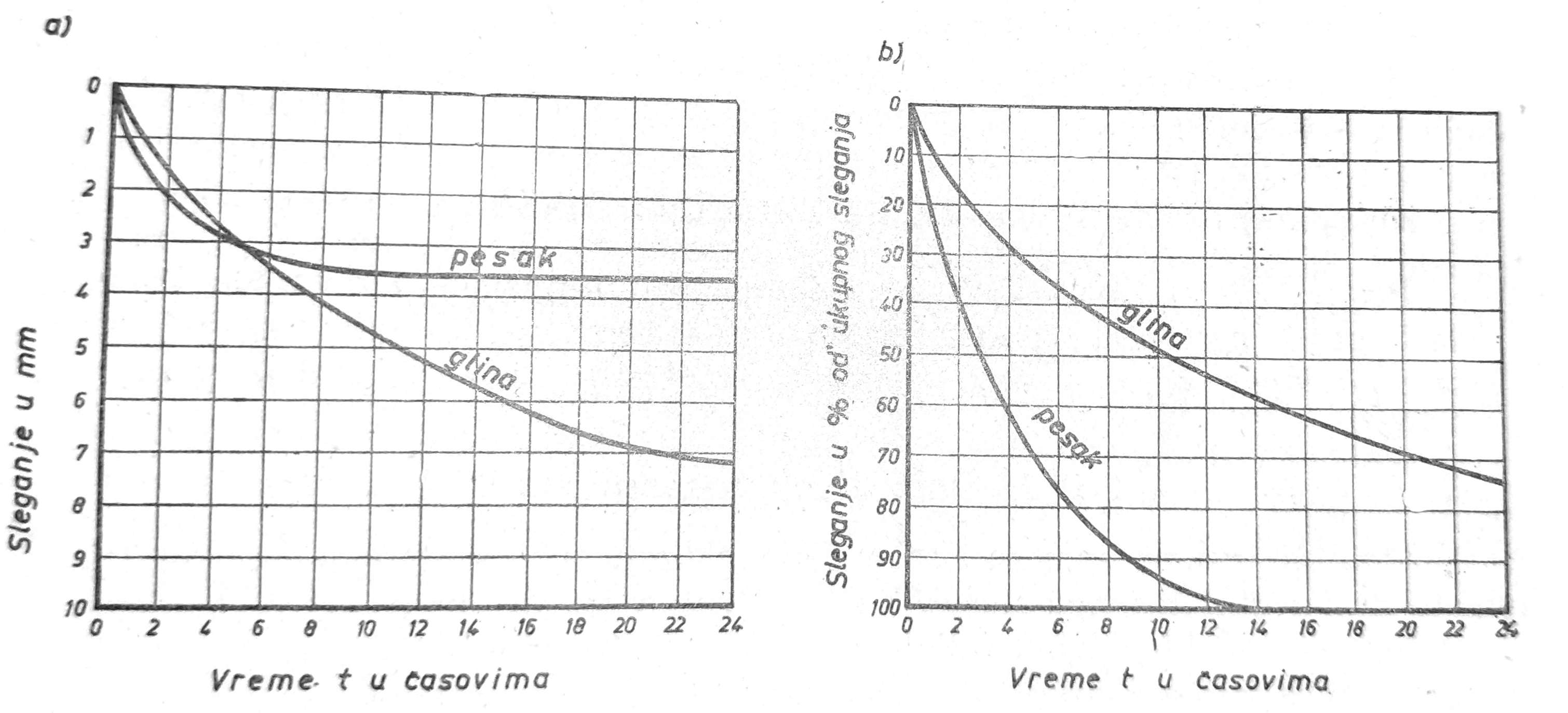
Sl. 6. Dijagram vremenskog sleganja
Pod dejstvom opterećenja nevezana i vezana tla se različito ponašaju. Nevezana tla, kao što je pesak, imaju krupne pore, iz kojih se pod opterećenjem voda brzo istiskuje, tako da se tlo brzo sleže, pri čemu se najveće sleganje obavlja u početku opterećenja i u relativno kratkom vremenskom intervalu dostigne konačno sleganje pri datom opterećenju. Vezana tla kao što je glina, imaju sitne pore iz kojih se voda teško istiskuje pod opterećenjem. U vremenskom procesu sleganja vezanog tla postoje dve faze. U prvoj fazi, odmah po nanošenju opterećenja na tlo, pošto voda iz pora ne može da ističe, ona postaje napregnuta i prima celo naneto opterećenje. U drugoj fazi, napregnuta voda u porama počinje da se istiskuje pod sopstvenim naponom usled opterećenja, koje se postepeno prenosi na čvrste čestice tla. U ovoj drugoj fazi nastaje zbližavanje čestica i smanjivanje pora. Proces sleganja traje sve dotle, dok traje istiskivanje napregnute vode iz pora, tj. dok ne prestane da postoji napregnuto stanje vode u porama. Prema tome konsolidacija tla je prvenstveno hidrodinamički problem, koji zavisi od propustljivosti tla i od njegove poroznosti. Kod gline, čija propustljivost je mala, proces konsolidacije može trajati vrlo dugo, a osim toga i sleganja mogu biti znatno veća zbog veće ukupne poroznosti nego kod peska. Na bazi opita konsolidacije može se vršiti proračun vremenskog toka sleganja za celo trajanje konsolidacije i u pojedinim fazama.