U mehanici tla određuju se granična nosivost tla i dozvoljeno opterećenje tla.
Granična nosivost tla je ona, koja se dostigne u trenutku kada nastupa lom tla. Lom tla nastaje kada opterećenje kojim temelj deluje na tlo prekorači njegovu čvrstoću smicanja. U tom slučaju, pod dejstvom opterećenja temelja P pojavljuju se površine najmanjeg otpora ACD i BCE – klizne površine sl. 1, po kojima se tlo bočno istiskuje i istovremeno dolazi do izdizanja tla iznad površine terena pored objekta DG i EF, dok sam temelj tone.
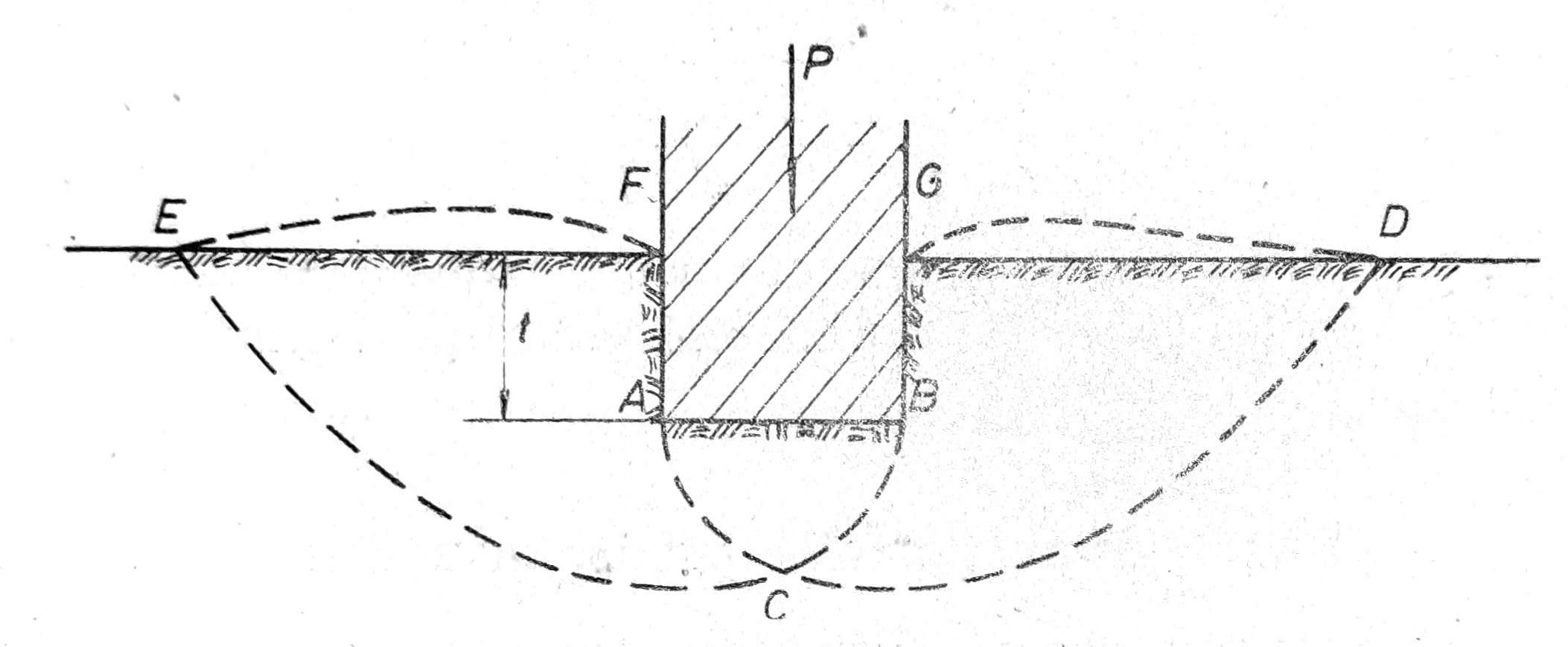
Sl. 1. Lom tla pod dejstvom opterećenja temelja
Čvrstoća smicanja tla povećava se sa dubinom fundiranja t, jer se usled težine gornjih slojeva smanjuje mogućnost bočnog istiskivanja. Prema tome, duboki temelji teže izazivaju lom tla, dok su plitki temelji opasni na lom. Isto tako široki temelji teže izazivaju lom tla, jer su klizne površine dublje.
Dozvoljeno opterećenje tla je ono koje se može dopustiti da deluje na tlo s tim, da se ne izazove lom tla pri najnepovoljnijim mogućim uslovima. Dozvoljeno opterećenje tla se određuje na osnovu granične nosivosti tla primenom faktora sigurnosti. Veličina faktora sigurnosti zavisi od više faktora, među kojima su najvažniji tačnost fizičkih karakteristika tla, mogućnost promena vrednosti elemenata unutrašnjeg otpora tla naročito kohezije, čija vrednost može da varira u širokim granicama pod dejstvom vode u tlu, zatim uticaj mogućih drugih faktora, kao što su uslovi opterećenja (mogućnost naglog i dinamičkog opterećenja), dubina fundiranja, i širina temeljne stope.
Nosivost tla može se odrediti na osnovu loma tla, koji daje graničnu nosivost. Pod graničnom nosivošću tla podrazumeva se veličina opterećenja koje izaziva lom. Postoje dva načina određivanja granične nosivosti na osnovu loma tla i to matematičko rešenje i probno opterećenje.
Matematičko rešenje
Mnogi naučnici pokušavali su da nađu matematičko rešenje za određivanje granične nosivosti tla, na bazi poznavanja uticajnih faktora i pod različitim pretpostavkama uslova loma. Uticajni faktori su fizičke karakteristike tla, koje se određuju laboratorijskim opitima na neporemećenim uzorcima tla, stanje podzemne vode, dubina fundiranja, veličina i oblik opterećene površine, kao i način opterećenja, tj. ravnomerno ili neravnomerno, centrično ili ekscentrično opterećenje tla. Pretpostavke o uslovima loma zasnovane su na teoriji plastičnosti i teoriji elastičnosti. Međutim savremene metode određivanja nosivosti tla zasnivaju se na teoriji plastičnosti, koja se kombinuje sa nekim uprošćenim pretpostavkama.
Ovde ćemo izneti nekoliko poznatih računskih metoda određivanja granične nosivosti, odnosno dozvoljenog opterećenja tla.
Obrazac Prandtl-Caquota
Ako je temeljna stopa AB fundirana na dubini t ispod površine terena, na ovoj dubini vlada kontaktni pritisak po usled opterećenja temelja i bočni pritisak p=γt usled težine tla iznad nivoa temeljne stope do površine terena (sl. 2).
Pod neposrednim dejstvom težine temelja, u trenutku prekoračenja granične nosivosti tla pojavljuju se prave površine klizanja AC i BC, koje zaklapaju ugao α = 45° + ϕ/2 sa opterećenom površinom. Ove klizne površine obrazuju aktivnu zemljanu prizmu ABC.
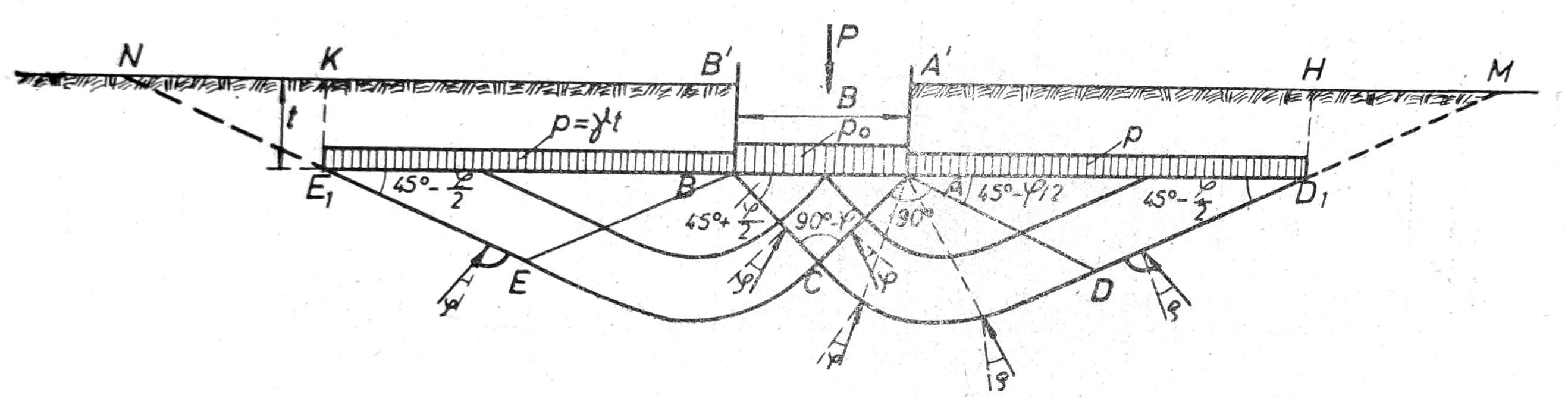
Sl. 2. Klizne površine oblika logaritamske spirale pod dejstvom centrično opterećene temeljne stope po Prandtl-Caquotu
Pod dejstvom pritiska aktivne zemljane prizme obrazuju se bočno pasivne zemljane prizme ADD1 i BEE1, koje ona teži da izgura naviše po površinama klizanja DD1 i EE1, pod uglom 45°-ϕ/2 sa horizontalom. Između zone aktivnog i pasivnog zemljanog pritiska postoji zona radijalnog smicanja ACD odnosno BCE, u kojoj pri prekoračenju granične ravnoteže klizanje nastaje po krivim kliznim površinama. Résal je izračunao, da su klizne površine u zoni radijalnog smicanja oblika logaritamske spirale sa polom u A odnosno B, čija je jednačina r=r0 eπ tgϕ
Za određivanje graničnog optrećenja tla učinjene su sledeće pretpostavke:
- da je temelj gladak, odnosno trenje između temeljne stope i tla zanemaruje se;
- da čvrstoća smicanja tla duž površina D1M i E1N ne postoji, odnosno zanemaruje se;
- da je zapreminska težina tla ispod temeljnog dna γ=0, odnosno zanemaruje se uticaj težine tla ispod temeljne stope, u zoni plastične ravnoteže.
Obrazac Prandtl-Caquota glasi:
Granična nosivost tla je
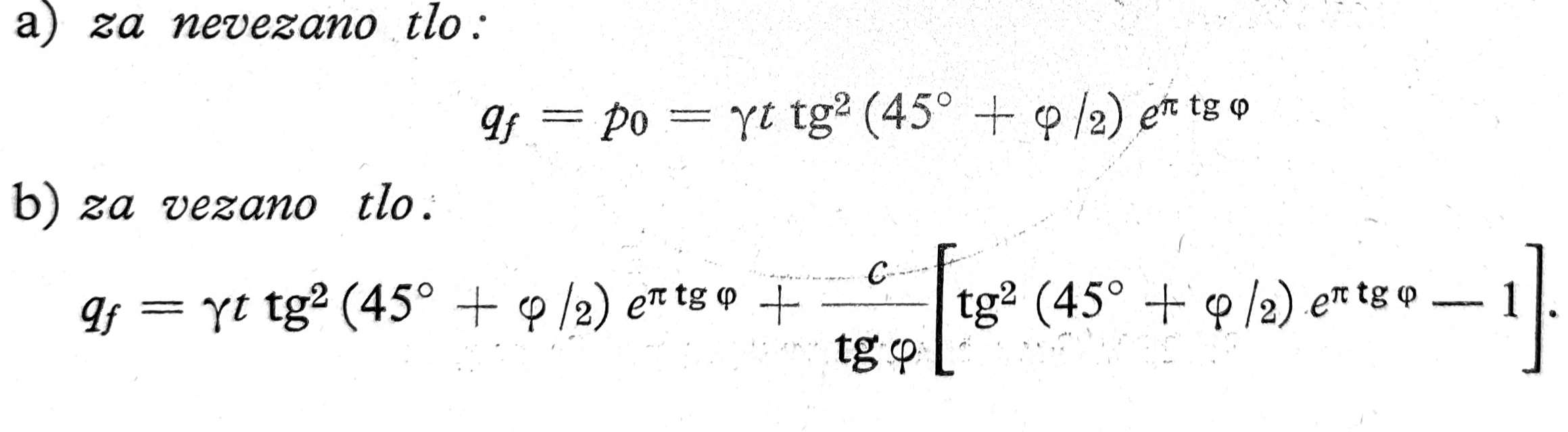
Ako stavimo:
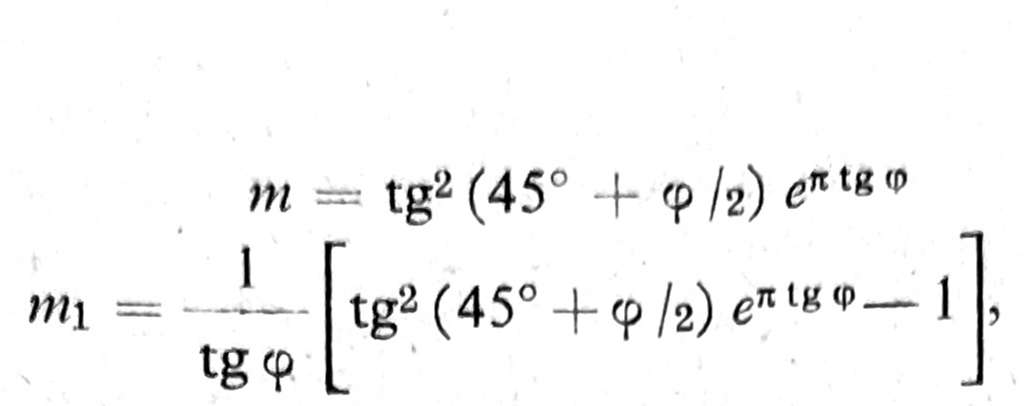
granična nosivost vezanog tla je qf = γtm + cm1.
Za različite vrednosti ugla unutrašnjeg trenja tla, vrednosti za m i m1 date su u tablici 1.
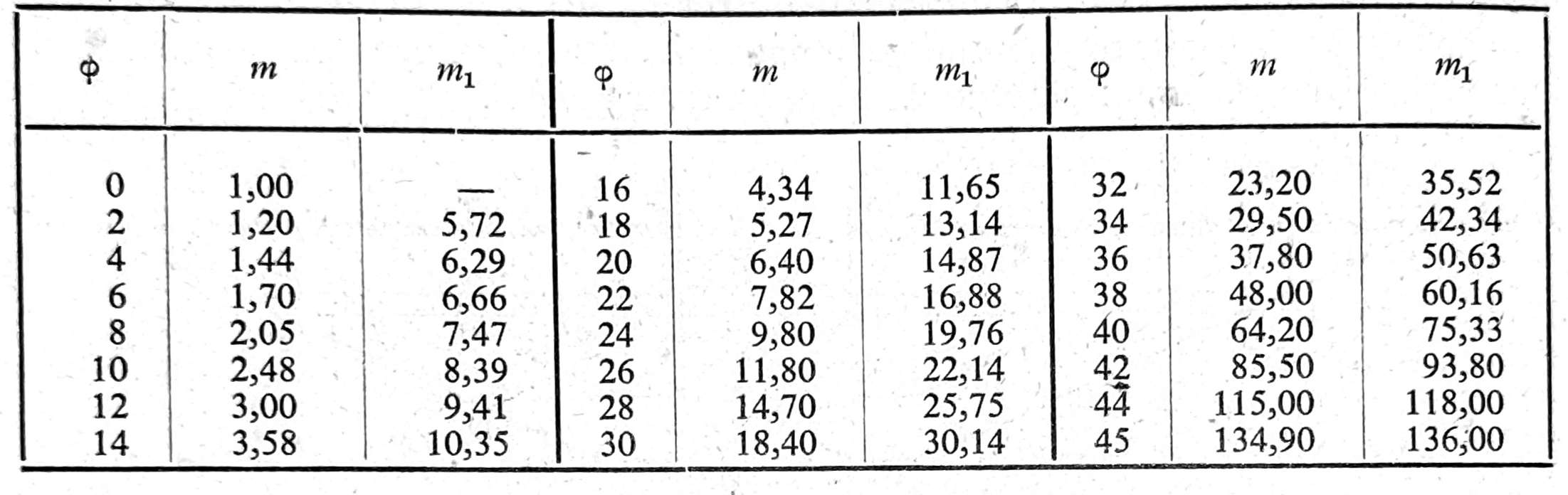
Tabl. 1. Vrednosti koeficijenata m i m1 za različite vrednosti ugla unutrašnjeg trenja tla
Dozvoljeno opterećenje tla je qa = pdozv = qf/F gde je F faktor sigurnosti. Za primenu Prandtl-Caquotovog obrasca usvaja se F = 4, te je qa = qf/4.
Terzaghiev obrazac
Terzaghi je dao poluempirički obrazac za izračunavanje granične nosivosti tla pod dejstvom opterećenja oblika trake, kvadrata i kružne ploče. On je posmatrao temelj fundiran na dubini Df ispod površine terena, širine B (sl. 3), te je usvojio da postoji trenje između temeljne stope AB i tla, koje se suprotstavlja bočnom istiskivanju tla i da površine klizanja AB i BC zaklapaju ugao unutrašnjeg trenja sa opterećenom površinom.
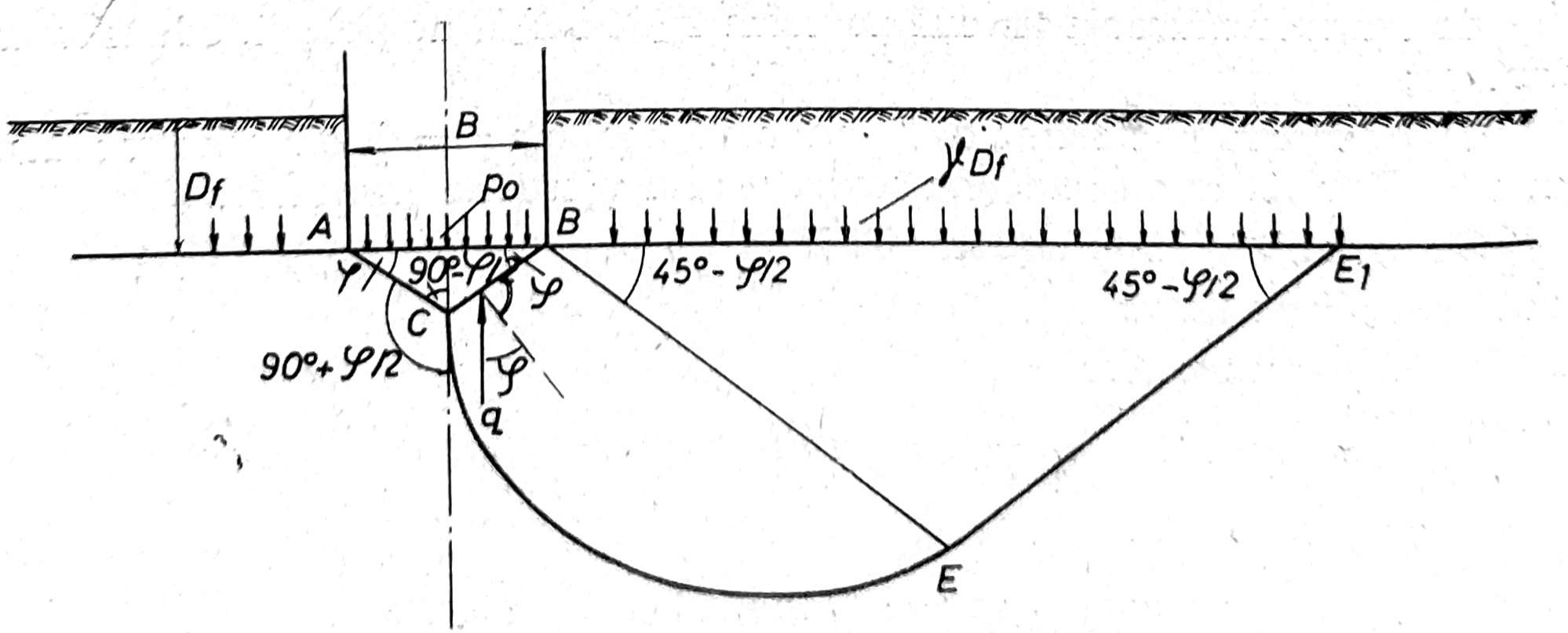
Sl. 3. Granična nostivost tla po Terzaghiu
Usled toga, tlo u zemljanom klinu ABC, obuhvaćeno između temelja AB i kliznih površina AC i BC ostaje u stanju elastične ravnoteže i ponaša se kao deo temelja. Prizma ABC ne može da se potisne sve dotle, dok pritisci na njegove strane AC i BC ne budu jednaki pasivnom zemljanom pritisku bočnih prizmi, što znači, da pri prekoračenju graničnog stanja ravnoteže rezultujući pritisak tla q deluje pod uglom ϕ prema normali na kliznu površinu, tj. u vertikalnom pravcu (sl. 3). Pošto se pod dejstvom opterećenja klin kreće vertikalno naniže, to se problem ravnoteže u tlu svodi na određivanje pasivnog zemljanog pritiska. Međutim pošto je tačan proračun nosivosti tla po ovoj metodi komplikovan, to je Terzaghi dao uprošćeno rešenje. Terzaghiev obrazac za izračunavanje granične nosivosti tla qf glasi
- Za temeljnu stopu oblika trake
qf = cNc + γ1 DfNq + 0,5 γ2 BNγ
gde je c kohezija tla
γ1 zapreminska težina tla iznad temeljnog dna
Df dubina fundiranja ispod površine terena do temeljnog dna
γ2 zapreminska težina tla ispod temeljnog dna
B širina temeljne stope.
Nc, Nq, Nγ su faktori nosivosti, zavisni od ugla unutrašnjeg trenja tla nosti ovog faktora dati su sledećim obrascima:
Nq je faktor usled težine bočnog sloja tla do dubine fundiranja: Nq = tg2 (45° + ϕ/2) eπ tgϕ
Nc je faktor usled kohezije: Nc = (Nq – 1) ctgϕ
Nγ je faktor usled sopstvene težine zemljanog klina ispod temeljne stope, odnosno ispod širine stope AB. Vrednost ovog faktora preporučuje Brinch Hansen kao približnu: Nγ ≈ 1,8 (Nq – 1) tgϕ
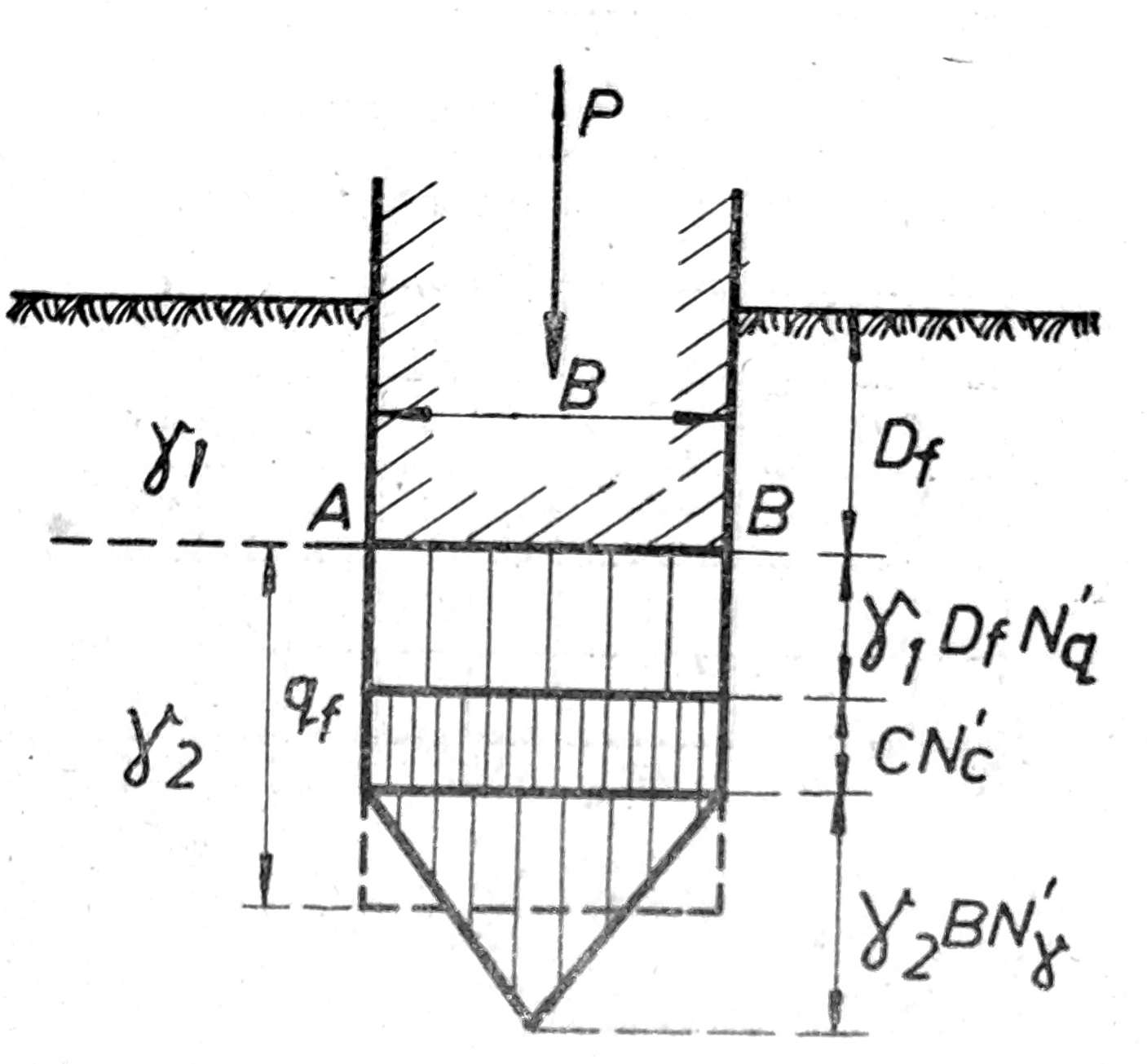
Sl. 4. Raspodela napona koje prima tlo pri vertikalnom centričnom opterećenju temelja
Zbog male razlike zapreminske težine tla često se usvaja γ1= γ2= γ. Prema prednjoj jednačini nosivost tla zavisi (sl. 4) od: kohezije temeljnog tla c, opterećenja tla pored temelja γ1 DF, sopstvene težine tla aktivne klizne prizme širine B.
Međutim dok je raspodela napona koje prima tlo usled dejstva kohezije c i dubine fundiranja Df ravnomerna na celoj širini, tj. pravougaona, dotle je raspodela napona koje prima tlo usled uticaja širine B trougaona, tj. najveći naponi se primaju u sredini temelja, i opadaju prema ivicama gde su jednaki nuli.
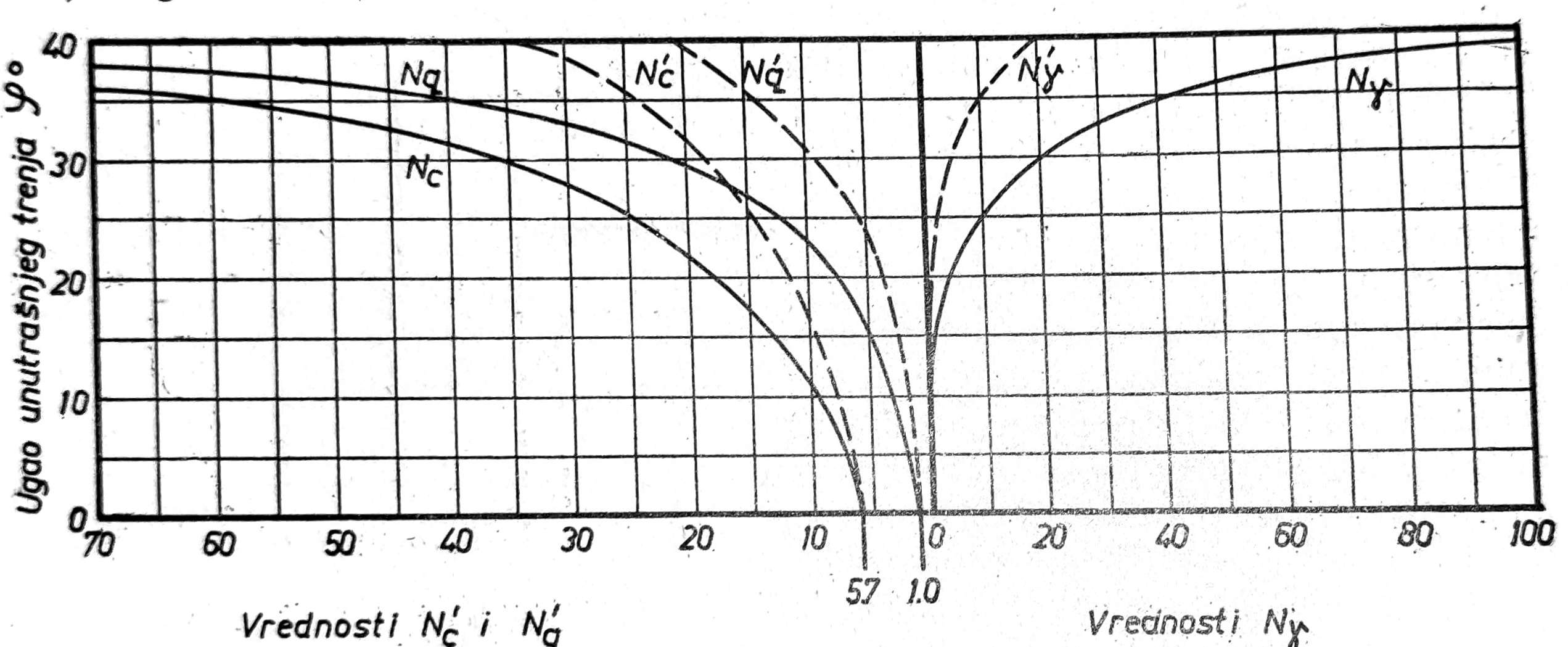
Sl. 5. Dijagram faktora nosivosti u zavisnosti od ugla unutrašnjeg trenja tla po Terzaghiu
Za različite vrednosti ugla od 0 do 40°, Terzaghi je izradio dijagrame faktora nosivosti (sl. 5). Međutim faktori nosivosti Nc, Nq i Nγ (pune linije na slici 5) mogu se usvojiti samo u slučaju zbijenog i čvrstog tla. Ako je tlo rastresito ili jače stišljivo, onda treba usvojiti faktore nosivosti N’c, N’q i N’γ (crtkane linije na sl. 5), koje daju 2/3 vrednosti otpora trenja. Pored toga u ovom slučaju treba uzeti 2/3 vrednosti kohezije c dobijene laboratorijskim putem, tako da u tom slučaju imamo qf = 2/3 cN’c + γ1 DfN’q + 0,5 γ2 BN’γ.
2. Za temeljnu stopu oblika pravougaonika
qf = 2/3 (1+0,3 B/L) cN’c + γ1 DfN’q + 0,5 γ2 BN’γ gde je L dužina temeljne stope
3. Za zemljanu stopu oblika kvadrata
qf = 2/3 1,3 cN’c + γ1 DfN’q + 0,4 γ2 BN’γ
4. Za temeljnu stopu kružnog oblika
qf = 2/3 1,3 cN’c + γ1 DfN’q + 0,6 γ2 rN’γ gde je r poluprečnik temeljne stope.
Za proračun dozvoljenog opterećenja tla usvaja se faktor sigurnosti F: qa = qf/F. Vrednost faktora sigurnosti kreće se od 2 do 3 prema uslovima tla i opterećenja.
Primena matematičkih obrazaca
Primena matematičkih obrazaca za određivanje dozvoljenog opterećenja tla zahteva poznavanje geomehaničkih karakteristika tla i to kohezije i unutrašnjeg trenja na dubini fundiranja i zapreminske težine tla iznad i ispod terneljnog dna. Ukoliko se temeljno tlo nalazi ispod nivoa podzemne vode, treba uzeti u obzir i uzgon pri određivanju zapreminske težine tla.
Kod većih opterećenja tla i većih objekata, kada se dobijena vrednost dozvoljenog opterećenja tla na osnovu matematičkih obrazaca potpuno iskorišćava, proračun nosivosti tla treba da bude propraćen proračunom sleganja. Izračunata nosivost tla usvaja se samo onda, ako je proračunom sleganja dobijeno manje sleganje od dozvoljenog za datu vrstu objekta. U slučaju ako je proračunom dobijeno sleganje veće od dozvoljenog, izračunata vrednost dozvoljenog opterećenja tla pomoću računskih obrazaca ne usvaja se, već se mora izmeniti način fundiranja tako, da se dobije manje sleganje, u granicama dozvoljenog sleganja za datu konstrukciju objekta.
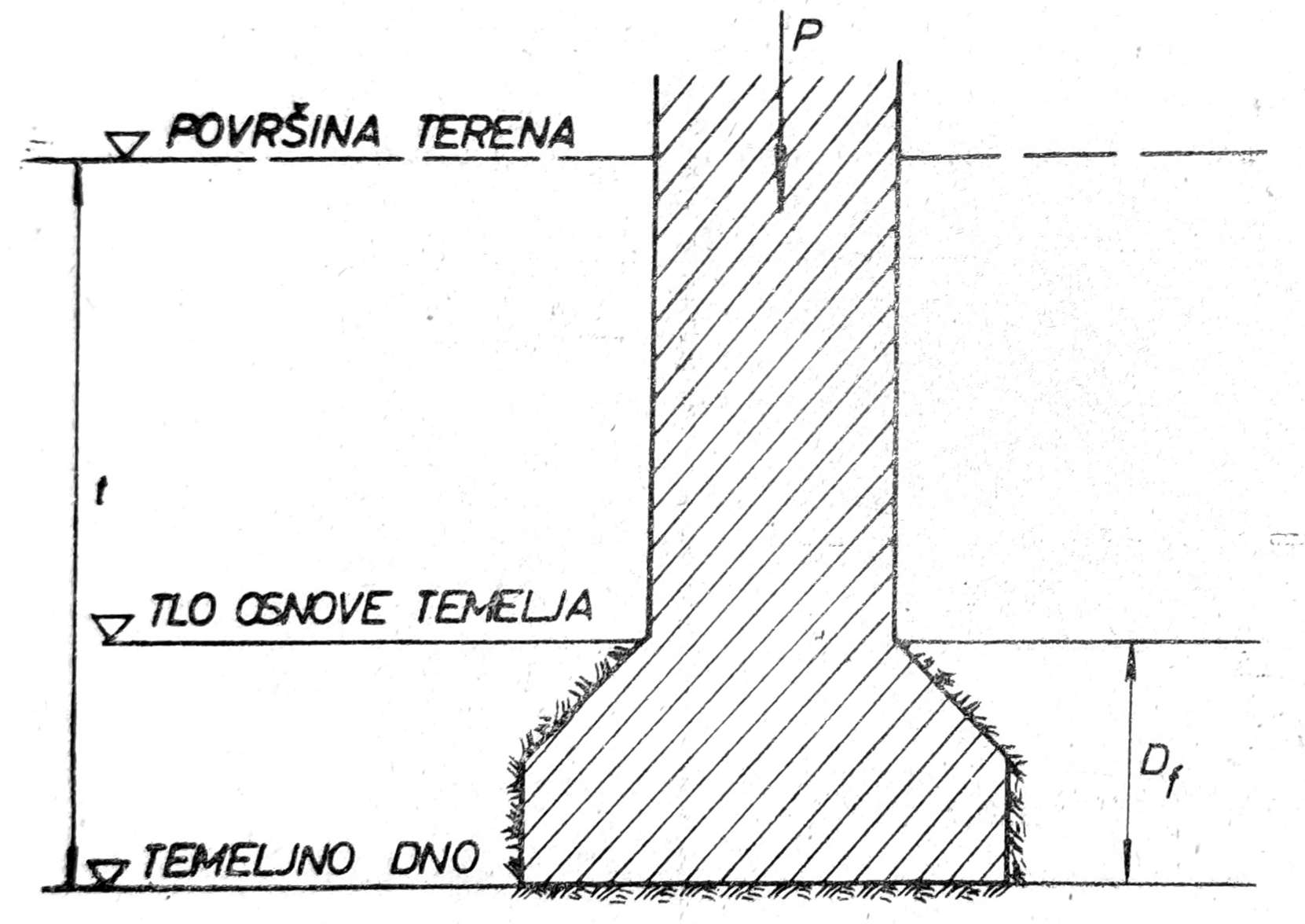
Sl. 6. Efektivna dubina fundiranja Df
U matematičkim obrascima za određivanje granične nosivosti tla nije vođeno računa o trenju omota temelja, koje takođe učestvuje kao otpor prema dejstvu opterećenja, ukoliko temelj čvrsto dodiruje tlo na bočnim stranama. Otpor trenja omota ne treba uzimati u obzir, jer stvarno trenje omota postoji samo kod šipova koji se pobijaju u tlo, dok je kod temeljnih stopa trenje omota neznatno, pošto se stope rade u unapred iskopanim jamama.
Primena matematičkih obrazaca kod kojih se ne vodi računa o obliku temelja daje najpribližnije rezultate za temelje oblika trake, tj. kada je dužina temelja više od dva puta veća od njegove širine. Opitima je utvrđeno, da kod temeljnih stopa oblika kvadrata ili kruga lom nastupa pri graničnom opterećenju koje je za 10-30% veće od izračunatog po matematičkim obrascima. Stope trouglog oblika daju manju nosivost od trake, a najmanju nosivost daju stope prstenastog oblika, ukoliko nisu ispunjene.
Dubina fundiranja Df računa se kao efektivna dubina fundiranja ispod tla osnove temelja do temeljnog dna (Sl. 6). Kod temelja ispod podzemnih prostorija, efektivna dubina fundiranja Df razlikuje se od dubine fundiranja i ispod površine terena. U takvim slučajevima, za proračun graničnog i dozvoljenog opterećenja tla treba uvek usvojiti Df, pošto je iznad tla osnove temelja vazduh koji se ne suprotstavlja bočnom istiskivanju tla pod dejstvom opterećenja temelja P.
