Kapilarnost i propustljivost tla

Kapilarnost

Pojava kapilarnosti

Ako usku staklenu cev potopimo u sud sa mirnom vodom bez toka, voda u cevi popeće se na visinu h_k iznad nivoa N u sudu, a površina vode u cevi obrazovaće menisk m (sl. 1a). Ukoliko je cev uža utoliko je visina kapilarnog penjanja vode h_k veća.

Kapilarno penjanje vode pripisuje se izdižućoj sili meniska m, a tumači se intermolekularnim privlačnim silama između molekula vode i stakla i površinskim naponima između zidova uske cevi i površine vode.

Na dodiru između zida staklene cevi i površine vode deluje kapilarna sila R u pravcu tangente na površinu meniska m, koja se izražava jedinicom težine na jedinicu dužine, u p/cm. Razlaganjem sile R u komponentu J paralelnu sa površinom zida i komponentu P normalnu na zid, dobijamo izdižuću silu meniska (sl. 1a):  J = R cosα.

Ugao α koji sila R zaklapa sa površinom zida zove se ugao kapilarnosti i njegova vrednost se kreće od 0 do 90^O. Ako su voda u kapilarnoj cevi i njeni zidovi potpuno čisti, onda je α=0, površina meniska je polukružna, izdižuća sila J = R je maksimalna (sl. 1b). Ako voda sadrži masti ili organske kiseline ili ako su zidovi masni, onda je α = 90°, ne dolazi do obrazovanja meniska, te nema ni kapilarnog penjanja vode.

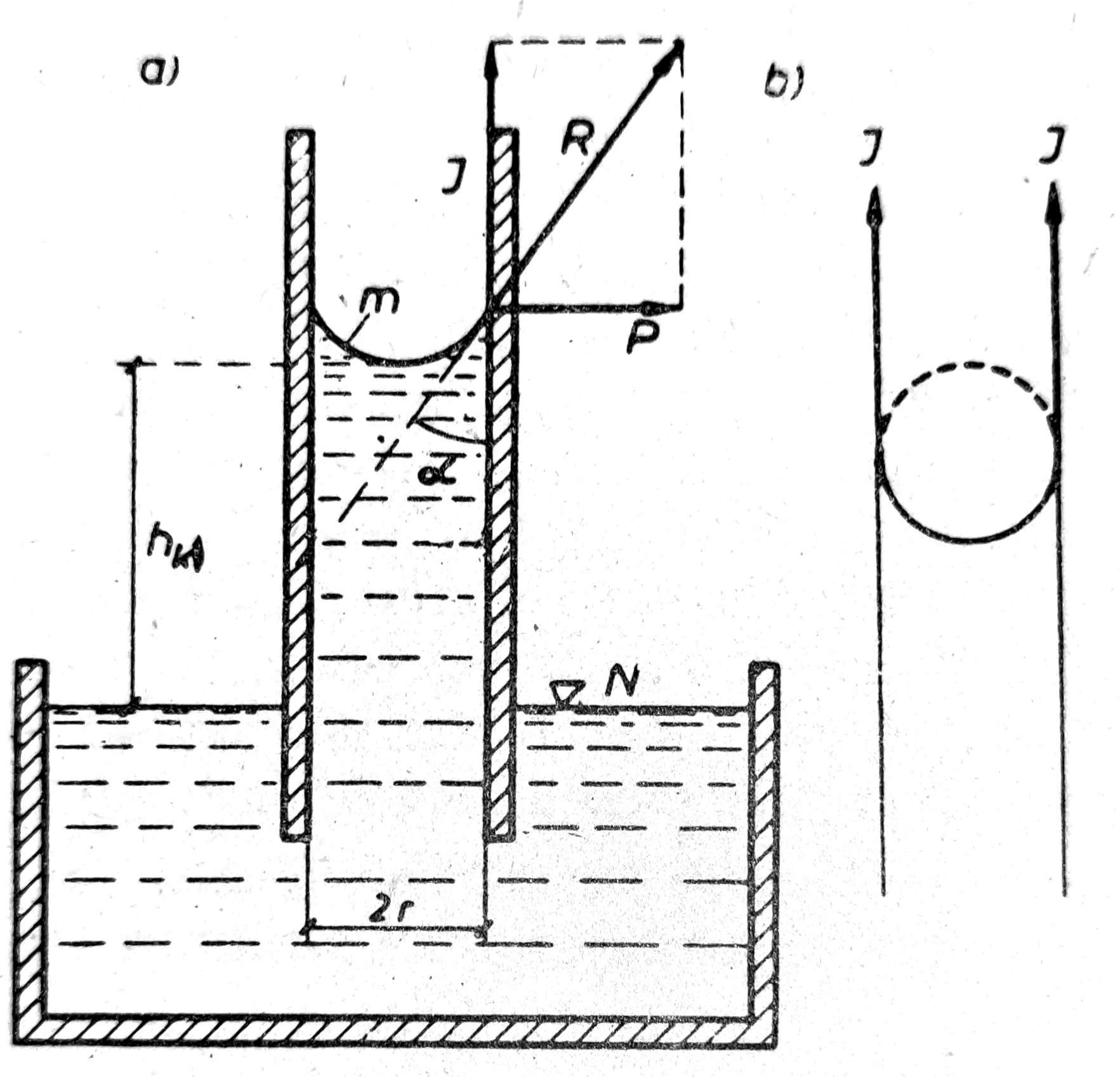
Sl. 1. Kapilarno penjanje vode i dejstvo kapilarnih sila

Izdižuću silu J = R cos α dobijamo iz uslova ravnoteže, prema kome ukupna izdižuća sila J na celom obimu meniska, odnosno kapilarne cevi poluprečnika r, drži vodeni stub u cevi visine hₖ:

R cos α · 2πr = πr² hₖ γ_w

gde je γ_w zapreminska težina vode.

Iz prednje jednačine dobijamo izdižuću kapilarnu silu:

R cos α = (r · hₖ · γ_w) / 2

odnosno visinu kapilarnog penjanja:

hₖ = (2R) / (r · γ_w) · cos α  [cm].

Topla kapilarna voda penje se u kapilarnoj cevi na veću visinu nego hladna zbog veće viskoznosti. Zbog toga je za istu visinu kapilarnog penjanja hₖ sila R cos α manja za toplu kapilarnu vodu nego za hladnu. Prema izvršenim opitima za različite temperature vode t pri svima istim uslovima dobijene su sledeće vrednosti izdižuće sile R cos α:

Voda u kapilarnoj cevi napregnuta je na zatezanje, jer je sila R cos α izdiže naviše, dok je sila gravitacije vuče naniže. Međutim zidovi kapilarne cevi napregnuti su na pritisak pod dejstvom kapilarne sile R.

Kapilarnost u tlu

Kapilarnost postoji i u tlu, gde kapilarne cevi sačinjavaju pore, koje su u međusobnoj vezi u svima pravcima. Ukoliko je tlo sitnozrnije, utoliko su pore sitnije i kapilarna visina penjanja je veća. Ova visina zavisi još i od strukture tla. Međutim pore u tlu mogu biti različite veličine i u tome slučaju i visina kapilarnog penjanja je različita. Ako kapilarna voda pri penjanju dostigne na „šira mesta“ tj. do veće pore nego što odgovara izdižućoj sili za prečnik uže pore na dostignutoj visini, onda dalje kapilarno penjanje zavisi od veličine te veće pore. U ovom slučaju imamo aktivnu kapilarnu visinu penjanja hₖₐ koja zavisi od najvećih pora. Naprotiv, kada pri spuštanju nivoa podzemne vode kapilarna voda silazeći odozgo naniže naiđe na „uža mesta“ ona će na toj dubini ostati i neće dalje silaziti. U tom slučaju imamo pasivnu kapilarnu visinu hₖₚ, koja zavisi od najmanjih pora.

Prema poroznosti i strukturi tla razlikuju se zatvorena i otvorena kapilarna voda.

Zatvorena kapilarna voda je u vezi sa ogledalom podzemne vode i pri penjanju potiskuje ispred sebe vazduh u gornju zonu tla. Usled toga povećava se količina vazduha u gornjoj zoni, a time i vazdušni pritisak, u porama te zone. Tako stvoreni vazdušni pritisak suprotstavlja se kapilarnom penjanju, te je visina kapilarnog penjanja manja. Ovaj slučaj nastupa u nižim slojevima tla, neposredno iznad nivoa podzemne vode, gde su pore sitne i pri kapilarnom penjanju voda potpuno ispunjava sve pore.

Otvorena kapilarna voda je takođe u vezi sa ogledalom podzemne vode, ali se nalazi pored pora ispunjenih vazduhom. Ovaj slučaj nastupa u gornjem delu tla gde su pore različite veličine tako da voda potpuno ispunjava samo sitne pore, dok se u susednim većim porama nalazi vazduh. Prilikom kapilarnog penjanja, voda istiskuje vazduh iz sitnih pora u susedne veće pore, tako da se u gornjoj zoni iznad vodenog stuba u kapilaru ne stvara vazdušni pritisak, te se otvorena kapilarna voda penje na veću visinu nego zatvorena.

Zona u kojoj postoji zatvorena odnosno otvorena kapilarna voda određuje se na osnovu količine vode w u tlu.

Kod zatvorene kapilarne vode sve pore su ispunjene vodom, što znači da je količina vode u tlu w = w_Z, odnosno da je stepen zasićenosti Sᵣ = 1,0.

Kod otvorene kapilarne vode sitne pore su potpuno ispunjene vodom, dok su veće pore delimično ispunjene vodom i to vodenim filmom koji obavija čvrste čestice i ugaonom vodom (sl. 2) na dodirnim mestima između čvrstih čestica, a delimično vazduhom, te je u ovom slučaju w < w_Z, odnosno Sᵣ < 1,0.

Visine kapilarnog penjanja hₖ za pojedine vrste tla određuju se laboratorijskim opitom. Prosečne visine hₖ za pojedine vrste tla kreću se u sledećim granicama:

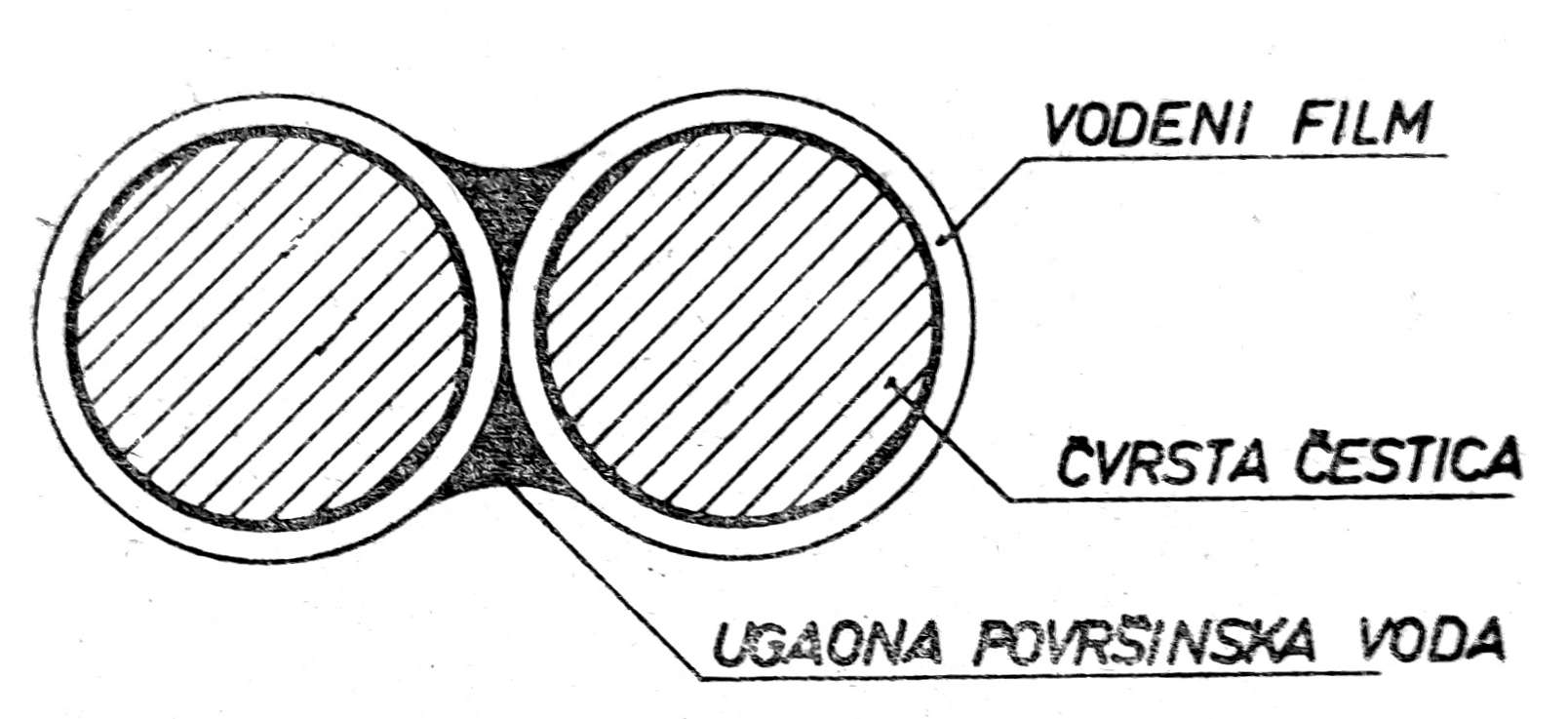
Sl. 2. Vodeni film i ugaona površinska voda

U tlu kapilarna sila R deluje pritiskom na čvrste čestice tako, da se između njih stvara tzv. prividna kohezija, koja deluje kao izvesna vezivost između čvrstih čestica. Međutim prividna kohezija postoji samo dotle, dok postoji kapilarno penjanje vode u porama tla. Potapanjem tla u vodu pore se zasićuju vodom i prividna kohezija prestaje da postoji.

Prividnom kohezijom tumači se pojava da sitan pesak, koji je u suvom stanju rastresit, u vlažnom stanju dobija izvesnu vezivost tako da se može modelirati što sa suvim peskom nije moguće.

Poznato je, da pesak (ukoliko nije mulj ili prašina) na morskim plažama kvašen talasima ima tako dobru nosivost, da se po njemu može voziti bicikl ili automobil, dok je malo dalje, gde ne dopiru talasi, isti pesak u suvom stanju i točkovi u njemu propadaju, tako da je svaka vožnja nemoguća.

PROPUSTLJIVOST

Proticanje vode kroz propustljivu masu

Posmatrajmo spojene sudove A, B, C, D, i E (sl. 3), čiji je jedan deo od a do b dužine L ispunjen propustljivom masom, na primer peskom. Ako na jednom kraju spojenih sudova sipamo vodu do nivoa N₁, onda će nivo vode u spojenim sudovima biti različit, tj. opadaće sa dužinom pređenog puta vode.

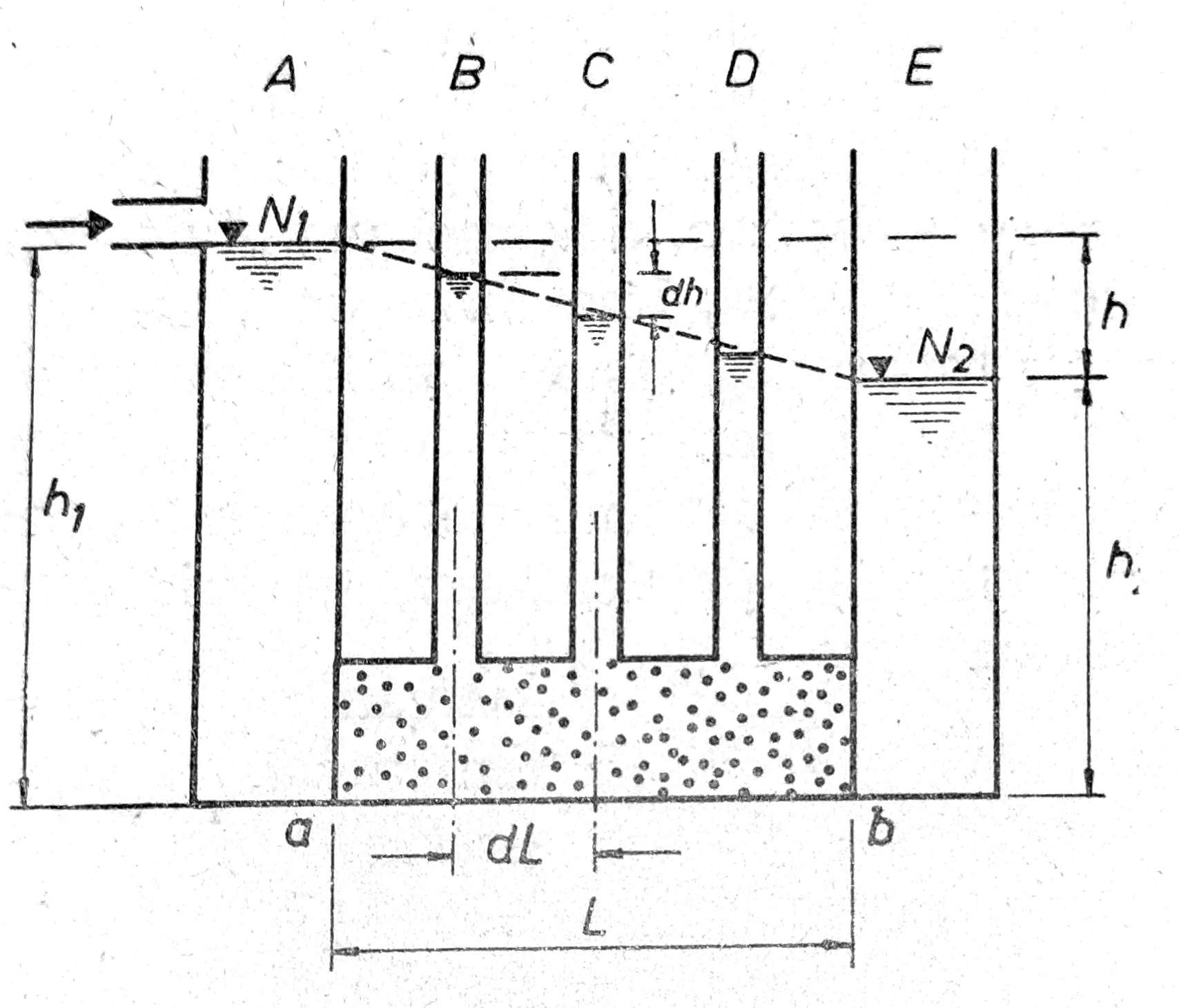
Sl. 3. Proticanje vode kroz propustljivu masu

U trenutku kada je ispred filtera dostignuta visina vodenog stuba h₁, iza filtera biće h₂. Razlika između nivoa N₁ i N₂ je tada:

h = h₁ − h₂

Razlika h predstavlja izgubljeni hidrostatički pritisak, koji je utrošen na savladivanje otpora proticanju vode kroz filter. Ovu pojavu utvrdio je francuski naučnik Darcy još 1856. god. On je tada postavio i sledeći obrazac za izračunavanje brzine proticanja vode kroz propustljivu masu:

V = k × (dh/dL) = ki

gde je:

• V = brzina proticanja vode kroz propustljivu masu, [cm/sec],
• k = koeficijent propustljivosti koji zavisi od osobina tla [cm/sec],
• dh = dužina koja se dobija kada se visina h podeli na veliki broj tankih slojeva [cm],
• dL = dužina koja se dobija kada se dužina L podeli na isti broj dužina kao i visina h, [cm].

Odnos dh/dL = i je odnos visine izgubljene u poniranju prema pređenom putu vode i zove se hidraulički pad, hidraulički gradijent ili još piezometarski nagib.
Ovaj poslednji naziv potiče od cevi B, C i D, koje se zovu piezometarske cevi. Prednji obrazac zove se Darcyev zakon kretanja vode kroz filter.

Ukupna količina vode q, koja u određenom vremenu t prođe kroz filter površine preseka A je

q = kAti,

odakle je

k = q / (Ati),  odnosno k = qL / Ath,

gde je i = h / L = hidraulički pad na dužini L (ako je on pravolinijski).

Koeficijent k izražava propustljivost tla pri temperaturi 10°C.

k = V / i  [cm/sec]

Brzina proticanja vode kroz tlo dobija se iz obrasca

V = q / A  [cm/sec],

gde je q = količina vode koja protiče kroz tlo u cm³ na sekundu, pri temperaturi od 10°C, A = površina preseka tla, kroz koju voda protiče, [cm²].

Darcyev zakon važi za laminarna kretanja vode, tj. mirna kretanja, bez vrtloga i za male brzine.

Filterska brzina V je srednja brzina kretanja vode kroz tlo i ona ne odgovara stvarnoj proticajnoj brzini vode, koja je veća. Pri proticanju vode kroz filter jednaki elementi proranja dh vrlo često su utrošeni na nejednakim dužinama puta vode dL, te je hidraulički gradijent promenljiv od jedne do druge tačke tla.

Propustljivost tla zavisi od veličine pora u njemu. Ako tlo izložimo opterećenju, pore se smanjuju i propustljivost postaje manja. Prema tome, za jedno isto tlo, koeficijent propustljivosti k upravo je proporcionalan sa veličinom poroznosti, odnosno sa njegovim koeficijentom poroznosti e. Međutim, za razne vrste tla, poroznost izražena koeficijentom poroznosti e ne može biti merilo za propustljivost, jer ova propustljivost zavisi ne toliko od ukupne poroznosti tla, koliko od veličine pora u njemu. Tako na primer šljunkoviti pesak čija poroznost iznosi e = 0,25, ima vrlo veliku propustljivost, k = 2–3 cm/sec, dok mekana glina, čija poroznost iznosi 60%, koeficijent poroznosti e = 1,50, ima malu propustljivost, k = 10⁻⁶ do 10⁻¹¹ cm/sec.

Koeficijent propustljivosti k može se odrediti računskim putem, laboratorijskim i terenskim opitima.

Određivanje koeficijenta na računskim putem zasniva se na granulometrijskom sastavu tla. Za određivanje koeficijenta k usvaja se pretpostavka da su čvrste čestice tla sferičnog oblika, što ne odgovara stvarnosti naročito kod koherentnog tla. Zbog toga se vrednosti koeficijenta k određene na ovaj način ne usvajaju kao tačne.

Određivanje koeficijenta k laboratorijskim opitima je najviše rasprostranjeno i vrše se na neporemećenim uzorcima tla. Međutim tačnost koeficijenta k određenog na ovaj način zavisi od više faktora kao što su, da li i u kojoj meri uzorak na kome se vrši opit reprezentuje propustljivi sloj u tlu, zatim od stanja neporemećenosti uzorka u aparatu za vršenje opita i od načina izvođenja opita. Ispitivanjem dovoljnog broja uzoraka koji će reprezentovati dato tlo, uzimanjem uzorka na terenu u cilindrima samog aparata za vršenje opita i odgovarajućim načinom izvođenja opita, mogu se dobiti približno tačne vrednosti koeficijenta k koje se mogu upotrebiti kao zadovoljavajuće.

Određivanje koeficijenta k terenskim opitom daje najtačnije vrednosti, jer potpuno odgovara sastavu i slojevitosti tla u kojima se ono nalazi. Međutim ovaj način određivanja koeficijenta k zahteva dosta vremena i velike troškove, zbog čega se on retko izvodi i to samo u slučajevima kada je njegova sasvim tačna vrednost neophodno potrebna.

Prema našim propisima za fundiranje smatra se da su tla čiji je koeficijent propustljivosti:

• k < 10⁻¹¹ cm/sec — skoro nepropustljiva
• k < 10⁻⁹        — vrlo malo propustljiva
• k < 10⁻⁷        — malo propustljiva
• k < 10⁻⁵        — srednje propustljiva
• k < 10⁻³        — jače propustljiva
• k > 10⁻³        — vrlo propustljiva