Pritisak na tunele sastoji se iz (sl. 1):
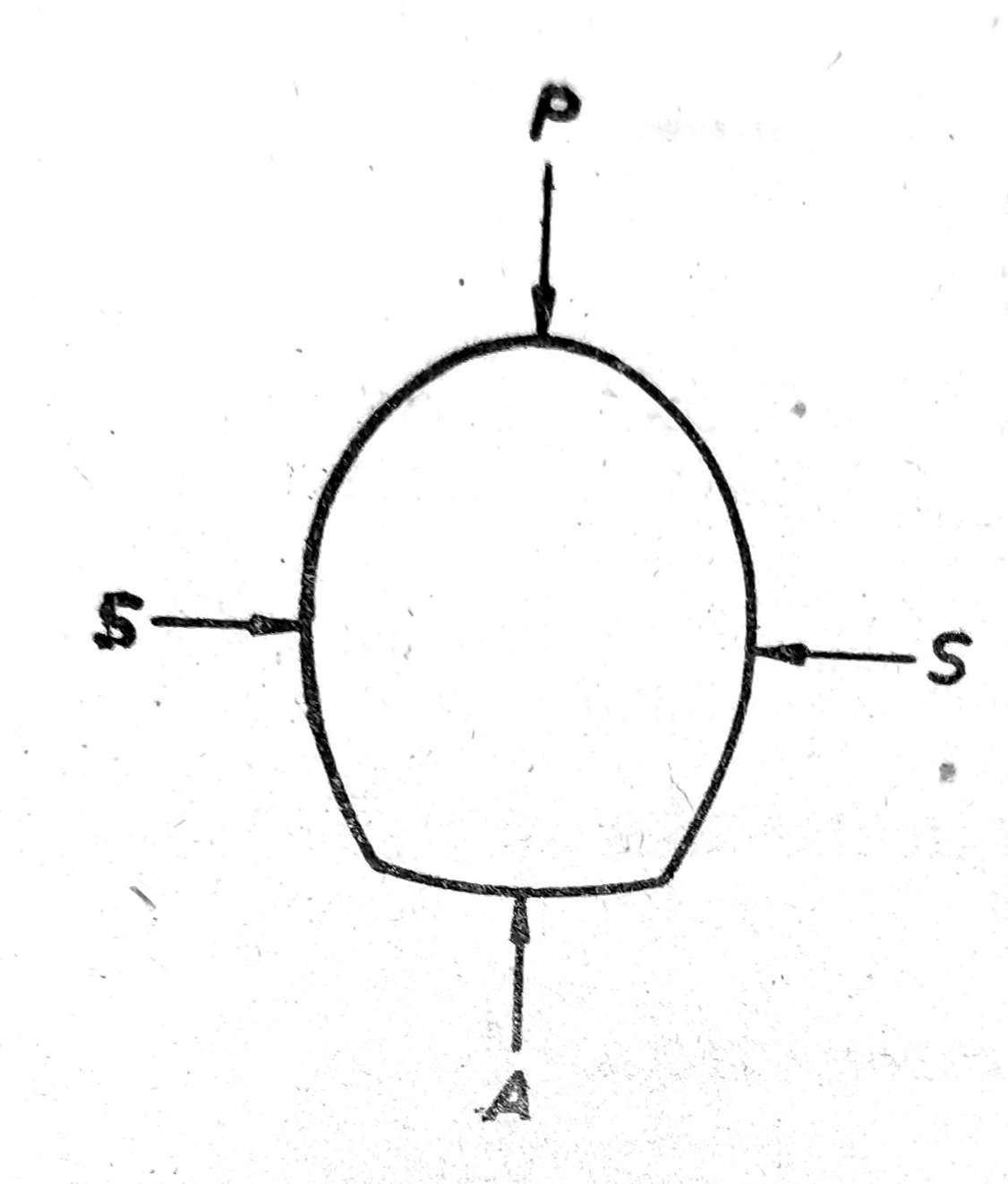
Sl. 1. Sile pritiska koje deluju na tunel
a) vertikalnog pritiska P na vrh, zvanog slemeni pritisak,
b) horizontalnog pritiska S, zvanog bočni pritisak,
c) reakcije na dno A, zvane podnožni pritisak.
Veličina zemljanog pritiska na tunel kreće se u vrlo širokim granicama. U početku, za vreme izbijanja tunela, brdski pritisak je relativno mali i kreće se od 0 do 0,50 kp/cm2, ali se po izbijanju povećava i kreće od 0,8 do 12,0 kp/cm2, u zavisnosti od vrste tla i njegovih fizičkih osobina, visine slojeva iznad tunela i od veličine pokreta u tlu koji nastaju kao posledica pritiska gornjih slojeva. Zbog zavisnosti od različitih faktora, određivanje brdskog pritiska na tunel je znatno otežano, tako da se teorijskim putem ne može odrediti tačna vrednost zemljanog pritiska, već samo približna. Protivu dejstva zemljanog pritiska na profil tunela suprotstavlja se unutrašnji otpor tla. Ako se tlo u kome se tunel radi sastoji od čvrste i kompaktne stene, pritisak na profil tunela je neznatan, jer težinu slojeva iznad tunela prima napon smicanja čvrste stene. U takvom slučaju nije potrebno raditi tunelsku oblogu niti podgradu za vreme izbijanja tunela, te otpada i određivanje zemljanog pitiska na profil tunela.
Kod nekompaktnih i trošnih stena, pritisak usled težine gornjih slojeva na profil tunela može prekoračiti čvrstoću ovakvih stena, usled čega dolazi do loma tla i jakih deformacija u profilu tunela. U ovakvim slučajevima treba raditi podgradu za vreme izbijanja tunela, a potom tunelsku oblogu koja će se suprotstaviti brdskom pritisku i prenositi ga preko fundamenta na niže slojeve.
U vezanom tlu unutrašnji otpor sastoji se iz kohezije i trenja, dok se u nevezanom tlu sastoji samo iz trenja bez kohezije. Međutim s obzirom na promenljivu vrednost kohezije pod uticajem vlage, kao i na slojevitost tla različitog sastava, kohezija se ne uzima u obzir kao unutrašnji otpor, te se i kod vezanog tla računa samo sa unutrašnjim trenjem. Stoga je u oba ova poslednja slučaja potrebna tunelska obloga, što znači da treba odrediti zemljani pritisak na tunel.
Za određivanje veličine zemljanog pritiska na tunel postoje sledeće pretpostavke:
1) Pretpostavka da zemljani pritisak raste proporcionalno sa dubinom
2) Pretpostavka zasnovana na zakonima ravnoteže trošnih tela
3) Pretpostavka o obrazovanju svoda rasterećenja u tlu
4) Pretpostavka zasnovana na zakonima elastičnosti.
Pretpostavka da pritisak raste proporcionalno sa dubinom
Po ovoj pretpostavci, na svod tunela (sl. 2) deluje slemeni pritisak P usled težine tla na celoj visini iznad tunela do površine terena, a na širini izbijenog tunela b. Prema tome, slemeni pritisak je
P = γ bt [Mp/m]
gde je γ zapreminska težina slojeva tla iznad tunela [Mp/m3], t visina slojeva tla iznad tunela [m].
Ova pretpostavka usvaja se samo u specijalnim slučajevima, kao što je na primer kada se tlo iznad tunela sastoji od mulja, koji nema gotovo nikakav unutrašnji otpor ili iz koherentnog i nekoherentnog tla u podzemnoj vodi, kada je otpor tla manji od dejstva težine tla.
Ovakvi slučajevi su u praksi retki i tretiraju se kao specijalni slučajevi. U svima ostalim slučajevima, kada se može računati sa unutrašnjim otporom tla, određivanje zemljanog pritiska na tunele po ovoj pretpostavci nije opravdano, jer ona daje mnogo veći pritisak od stvarnog.
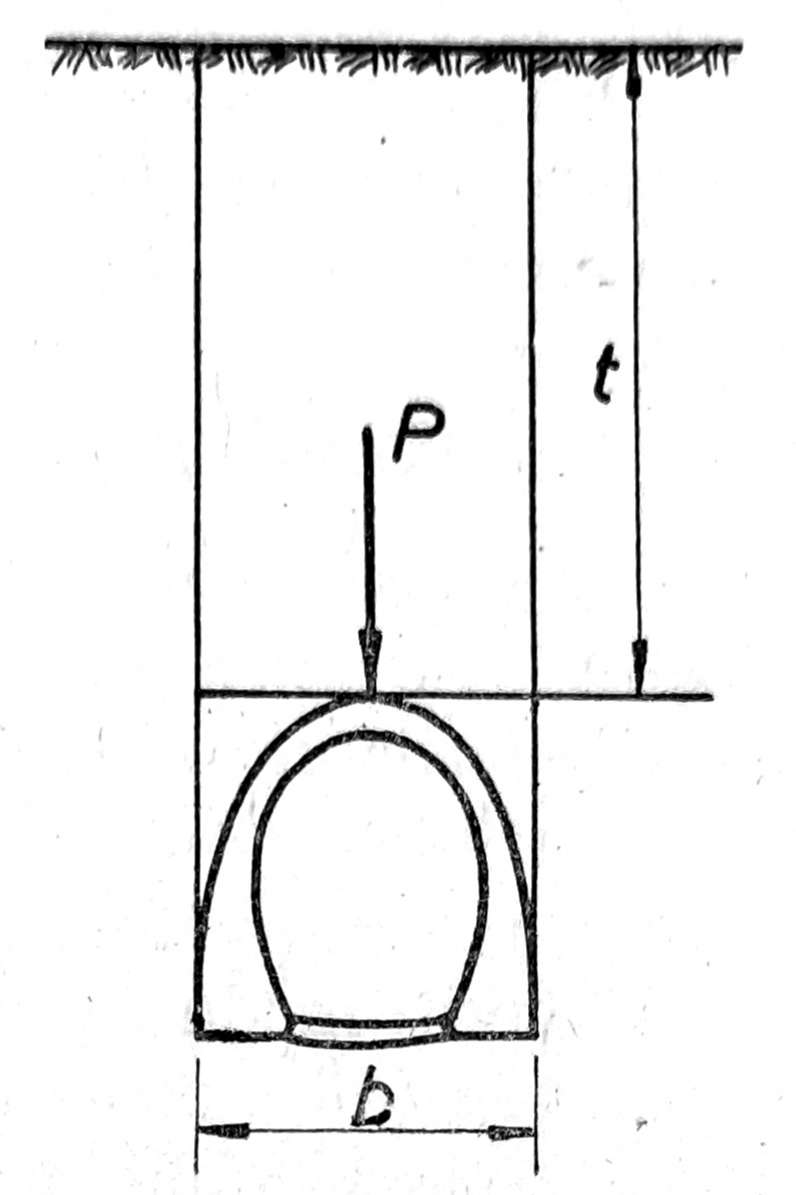
Sl. 2. Određivanje zemljanog pritiska na tunel pod pretpostavkom da pritisak raste poporcionalno sa dubinom
Pretpostavka zasnovana na zakonima ravnoteže trošnih tela
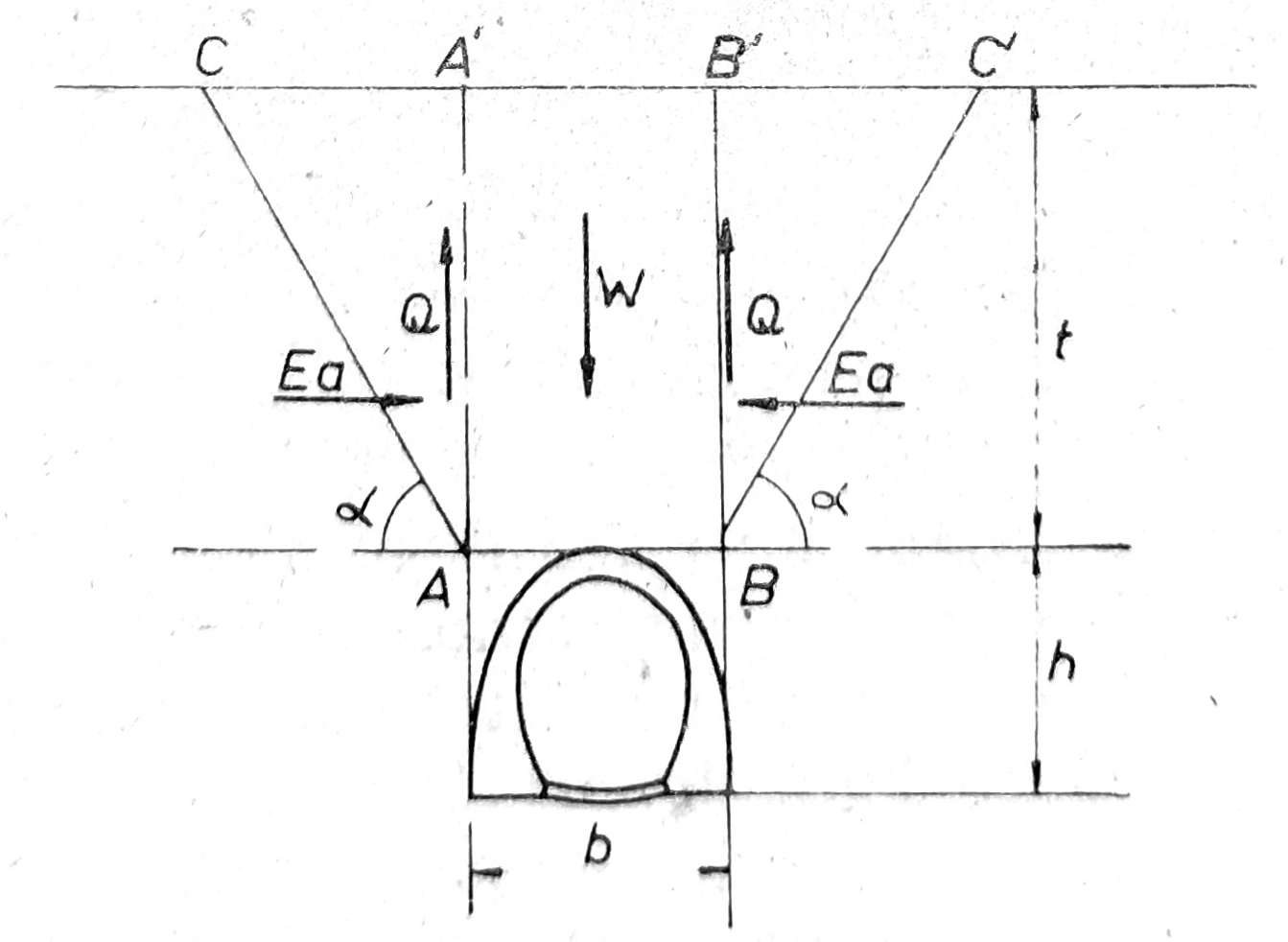
Sl. 3. Određivanje zemljanog pritiska na tunel po pretpostavci zasnovanoj na zakonima ravnoteže trošnih tela
Po ovoj pretpostavci posmatra se suvo trošno tlo i usvaja se da je pritisak na svod tunela manji od težine prizme ABA'B' zbog dejstva sile trenja u vertikalnim površinama AA' i BB' (sl. 3).
Na ovoj pretpostavci zasnovano je više obrazaca za izračunavanje pritiska na svod tunela, kao što su Forcheimerov, Bierbaumerov i Engesserov.
Ukupna težina tla iznad svoda tunela je W= γ bt, ali prizma ABA'B' neće moći slobodno da kliza naniže, jer će se ovom klizanju suprotstaviti trenje materijala u površinama AA' i BB'. Ako je o ugao unutrašnjeg trenja tla iznad svoda tunela, koeficijent trenja je tgo, a normalni pritisak na površinu trenja je ustvari bočna sila E, aktivni zemljani pritisak na površine AA' i BB'. Prema tome na svaku od ovih površina deluje sila trenja
Q = Ea tgϕ.
Pritisak P na svod tunela, slemeni pritisak, je
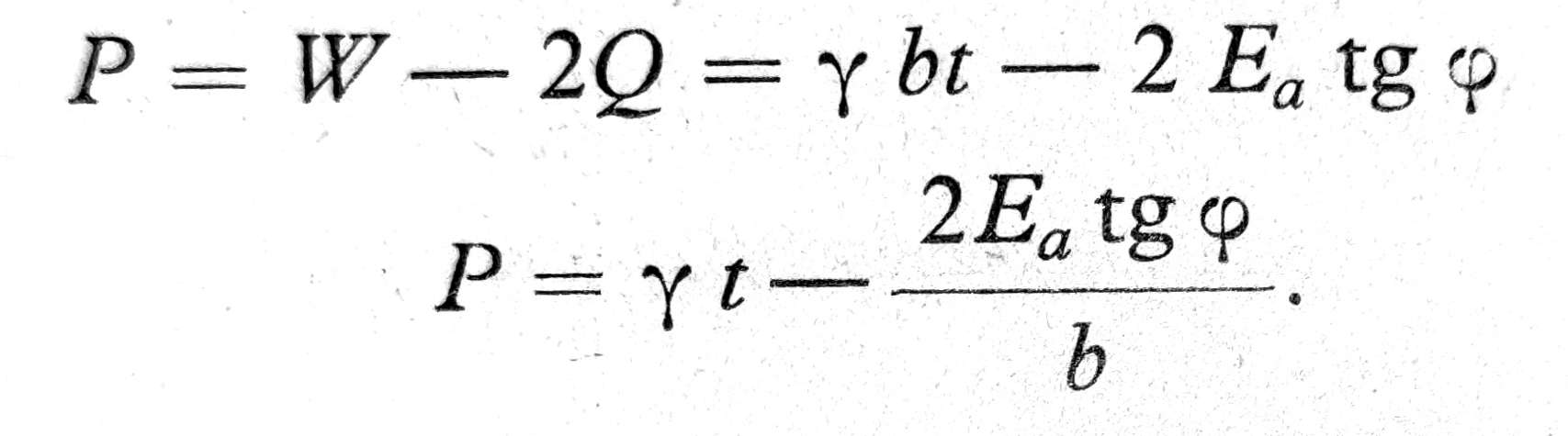
Aktivni zemljani pritisak računa se po Rankineu
Ea = ½ γt2 tg2(45o – ϕ/2)
Određivanje zemljanog pritiska na tunel po ovoj pretpostavci vrši se retko i samo u izvesnim slučajevima, kao što je na primer kada je visina slojeva tla iznad tunela mala, tako da se ne može obrazovati svod rasterećenja.
Pretpostavka o obrazovanju svoda rasterećenja
Po ovoj metodi, u svakom koherentnom i nekoherentnom tlu, izuzev u mulju, iznad tunela obrazuje se svod rasterećenja, tako da na profil tunela deluje samo materijal ispod tog svoda, dok se sam svod drži u ravnoteži usled lučnog dejstva, što je dokazano opitima u rastresitom peskovitom tlu. Za određivanje zemljanog pritiska na tunel po ovoj pretpostavci postoji više metoda među kojima su najpoznatije Kommerellova i Protođakonova. Po Kommerellovoj metodi usvaja se da svod rasterećenja ima oblik poluelipse, a po Protođakonovoj oblik parabole.
Kommerellova metoda poluelipse pritiska
Po ovoj metodi usvaja se, da visina svoda rasterećenja h zavisi od širine tunela bi od ugla unutrašnjeg trenja tla u kome se tunel izbija (sl. 4). Visina svoda rasterećenja h može se odrediti na osnovu obrasca:
h = 100a/p
gde je a sleganje podgrade od početka izbijanja tunela do završenog zidanja tunelske obloge, p trajna rastresitost tla.
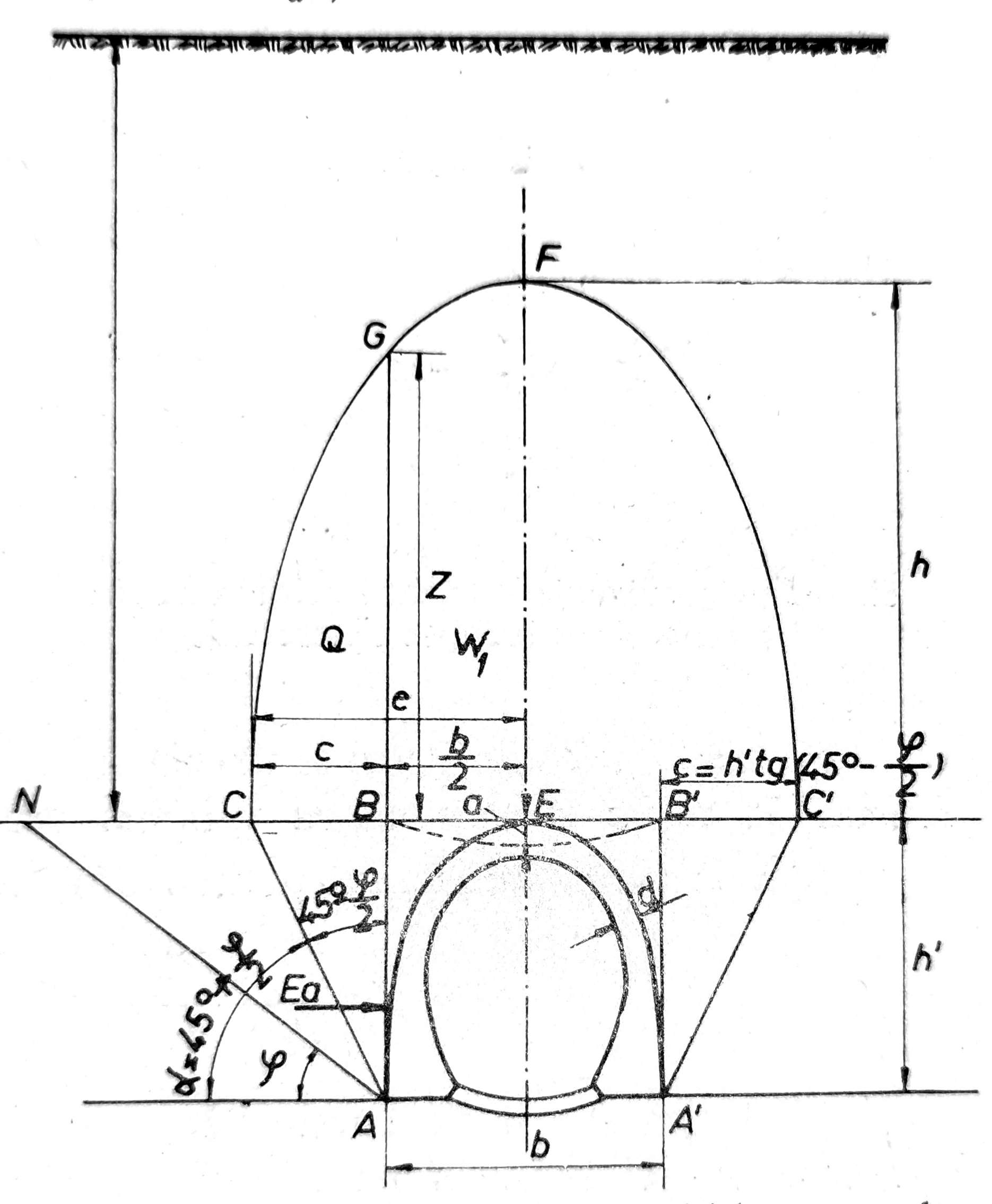
Sl. 4. Određivanje zemljanog pritiska na tunel po metodi poluelipse pritiska
Pri povoljnim uslovima usvaja se a = 10 – 15cm, pri nepovoljnim a = 15 – 40cm, pri vrlo nepovoljnim a = 40 – 70cm.
Trajna rastresitost tla p određuje se na iskopanom tlu tunela u % posle kopanja i ponovnog nabijanja. Vrednosti za p kreću se u granicama datim u tablici 1.
Međutim i ako je gornji obrazac dosta često primenjivan u praksi, smatra se da ne odgovara stvarnosti. Sleganje a nema apsolutnu vrednost, već je u jednom istom materijalu različito prema vrsti podgrade. Ako je podgrada čelična, sleganje je manje, ako je drvena sleganje je veće. Za normalne profile tunela na željezničkim prugama i putevima usvaja se za visine sloja tla iznad tunela t > 20 m da je visina svoda rasterećenja h=20 m.
Bočni pritisak. Po Kommerellu bočni pritisak nastaje usled dejstva težine zemljane prizme ABC (sl. 4), koja je ograničena sa bočnih strana kliznom površinom AC i vertikalnom ravni tunela AB, dok je sa gornje strane opterećena težinom zemljane prizme CBG. Pri tome se usvaja, da je aktivna zemljana prizma ograničena sa gornje strane horizontalnom površinom CB u ravni temena svoda tunela

Tabl. 1. Približne vrednosti tla p u %
Pošto je ravan AB vertikalna, ravan CB horizontalna, to se usvaja da postoji Rankineov slučaj zemljanog pritiska, te da je pravac aktivnog zemljanog pritiska E horizontalan. Po Rankineu je nagib klizne površine AC prema horizontali pod uglom α=45o+ϕ/2, aktivni zemljani pritisak Ea je
Ea = ½ γh2tg2(45o-ϕ/2),
gde je γ zapreminska težina tla u Mp/m3, h visina potpornog zida u m, ϕ ugao unutrašnjeg trenja tla.
Kako aktivnu zemljanu prizmu ABC opterećuje sa gornje stra ne težina prizme CBG, to će u ovom slučaju biti za visinu tunela h’
Ea = ½ γ h’ 2tg2(45o-ϕ/2),
gde je γ1 = γ + 2p/h’
pri čemu je p = Q/CB = Q/h’tg(45o- ϕ/2)
Težina Q dobija se kao razlika težine W četvrtine elpise pritiska CEF i težine W1:Q = W – W1.
Težina W dobija se iz površine A četvrtine elipse i zapreminske težine tla γ, W = Aγ. Površina A dobija se na osnovu jednačine površine elipse: A = h·e·π/4
Unoseći vrednost za p u jednačinu za Ea dobijamo:
Ea = ½ γ h’2 tg2 (45o-ϕ/2) + Q tg(45o-ϕ/2).
Slemeni pritisak. Pošto je svod rasterećenja simetričan u odnosu na vertikalnu osovinu, to se može računati slemeni pritisak za polovinu profila tunela. Težina W1 zemljane prizme BEFG za dužinu tunela 1,00 m je:
W1 = (z+h)/2 · b/2 · 1,00 · γ
U ovoj jednačini sve je poznato izuzev z, koje odredujemo na osnovu jednačine elipse (sl. 5): b2x2 + a2y2 = b2a2. U našem slučaju je b=e; a=h; x=z;
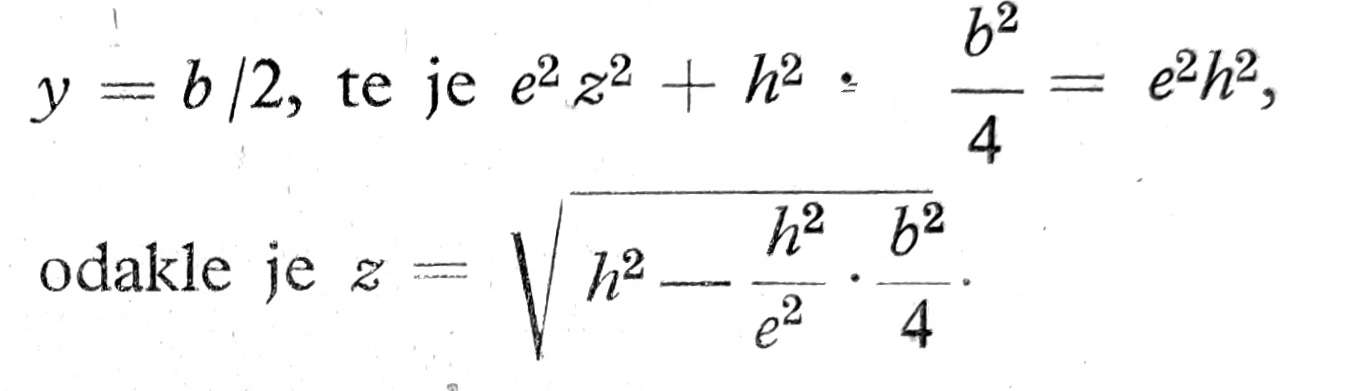
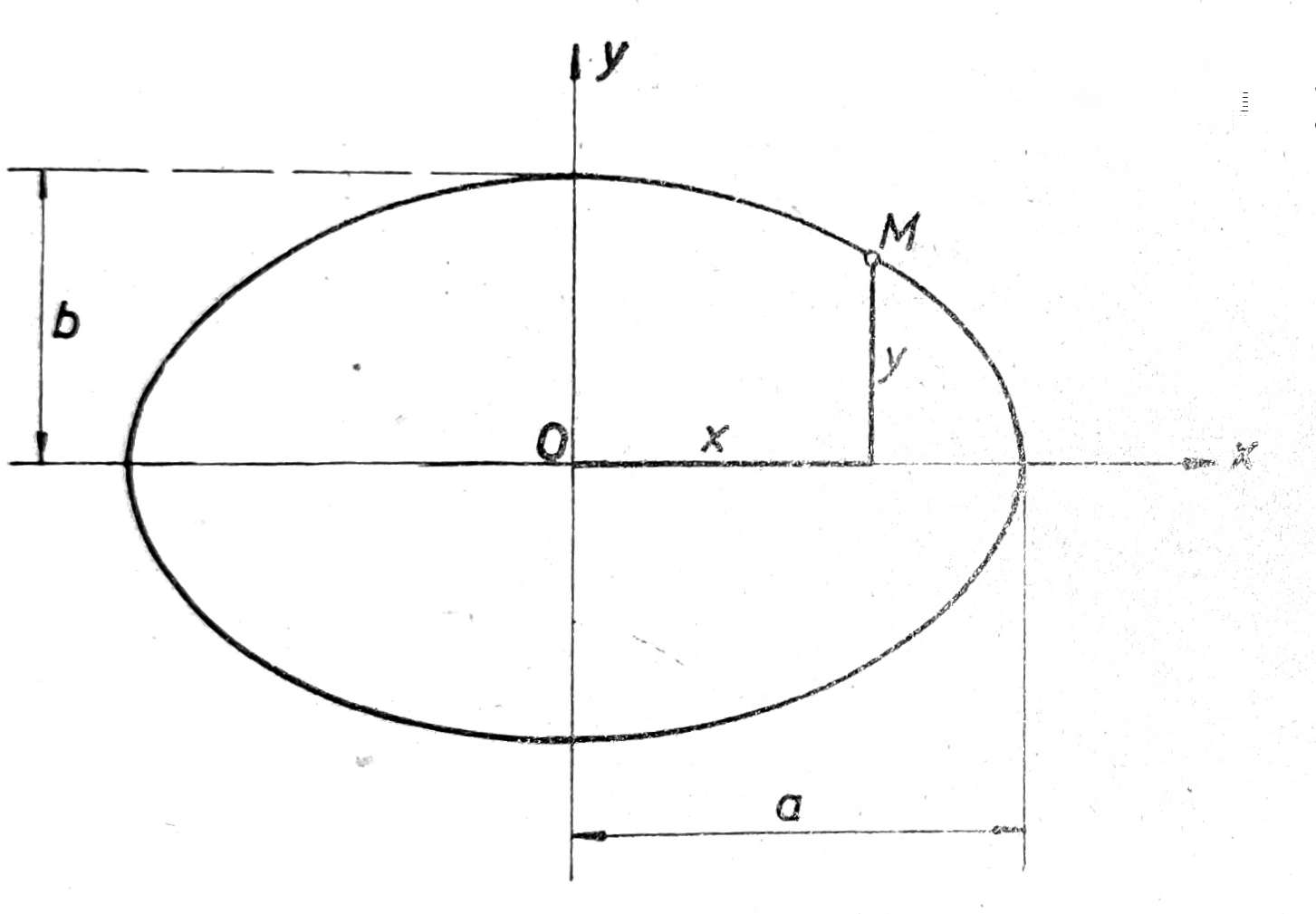
Sl. 5. Određivanje slemenog pritiska na tunel po metodi poluelipse opterećenja
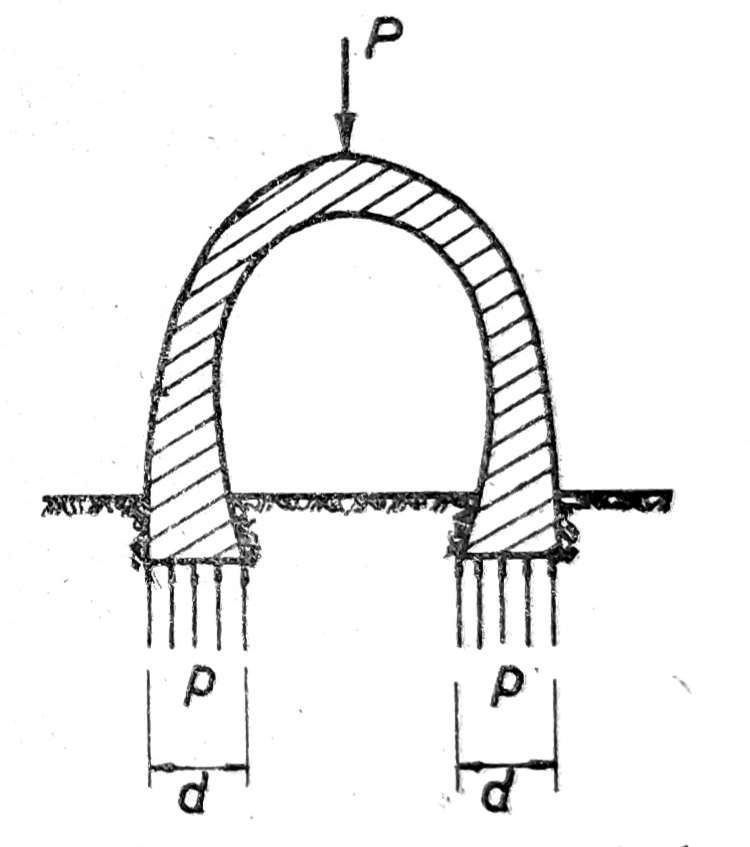
Sl. 6. Podnožni pritisak p ispod oporca
Podnožni pritisak. Pošto se usvaja da je podnožni pritisak A jednak slemenom pritisku P, to je time njegova veličina određena.
Ako je profil tunela sa podnožnim svodom, pritisak na dno tunela p je: p = P/(b·1,00m) [Mp/m2].
Medutim ako je to čvrsto i ima dovoljno veliku nosivost, slemeni pritisak P prenose oporci širine d na tlo (sl. 6), te je podnožni pritisak ispod oporaca: p = P/(2d·1,00m) [Mp/m2].
Napominje se da je u ovom slučaju neophodno izvršiti sondiranje terena i određivanje nosivosti i sleganja tla, jer se dešavalo da je nosivost tla manja od podnožnog pritiska, usled čega je dolazilo do deformacije tunelske obloge i sleganja celog tunelu.
Pretpostavka zasnovana na zakonima elastičnosti
U novije vreme pojavila se nova pretpostavka, da se tlo posmatra kao homogeno elastično izotopno telo na koje se mogu primeniti zakoni elastičnosti. Po ovoj pretpostavci, elastične osovine tla izražavaju se njegovim modulom elastičnosti E i Poissonovim koeficijentom µ koji zavisi od fizičkih osobina tla. Međutim u stvarnosti tlo nije izotropna, već je anizotropna masa, čije vrednosti modula E i koeficijenta µ se menjaju sa dubinom. Ipak i pored ovog odstupanja, primena teorije elastičnosti za određivanje zemljanog pritiska ima veliki naučni interes i perspektive za buduća ispitivanja.
Ispitivanje stabilnosti tunelske obloge pod dejstvom zemljanog pritiska
Za ispitivanje stabilnosti tunelske obloge izabere se poprečni presek obloge, pri čemu je korisno poslužiti se primerima ranije izrađenih tunela pod sličnim uslovima kao i u datom slučaju, koji su se održali u dobrom stanju, ili se pak odredi presek tunelske obloge po nekoj empiričnoj metodi (sl. 7a). Izabrani presek tunelske obloge podeli se u lamele po mogućstvu iste širine Δs. Za svaku lamelu odredi se vertikalni i bočni pritisak, kao i težina same lamele.
Vertikalni pritisak PG na lamelu za dužinu tunela 1,00 m (sl. 7a) dobija se na osnovu obrasca:
PG = (y1+y2)/2 · Δx·1,00·γ
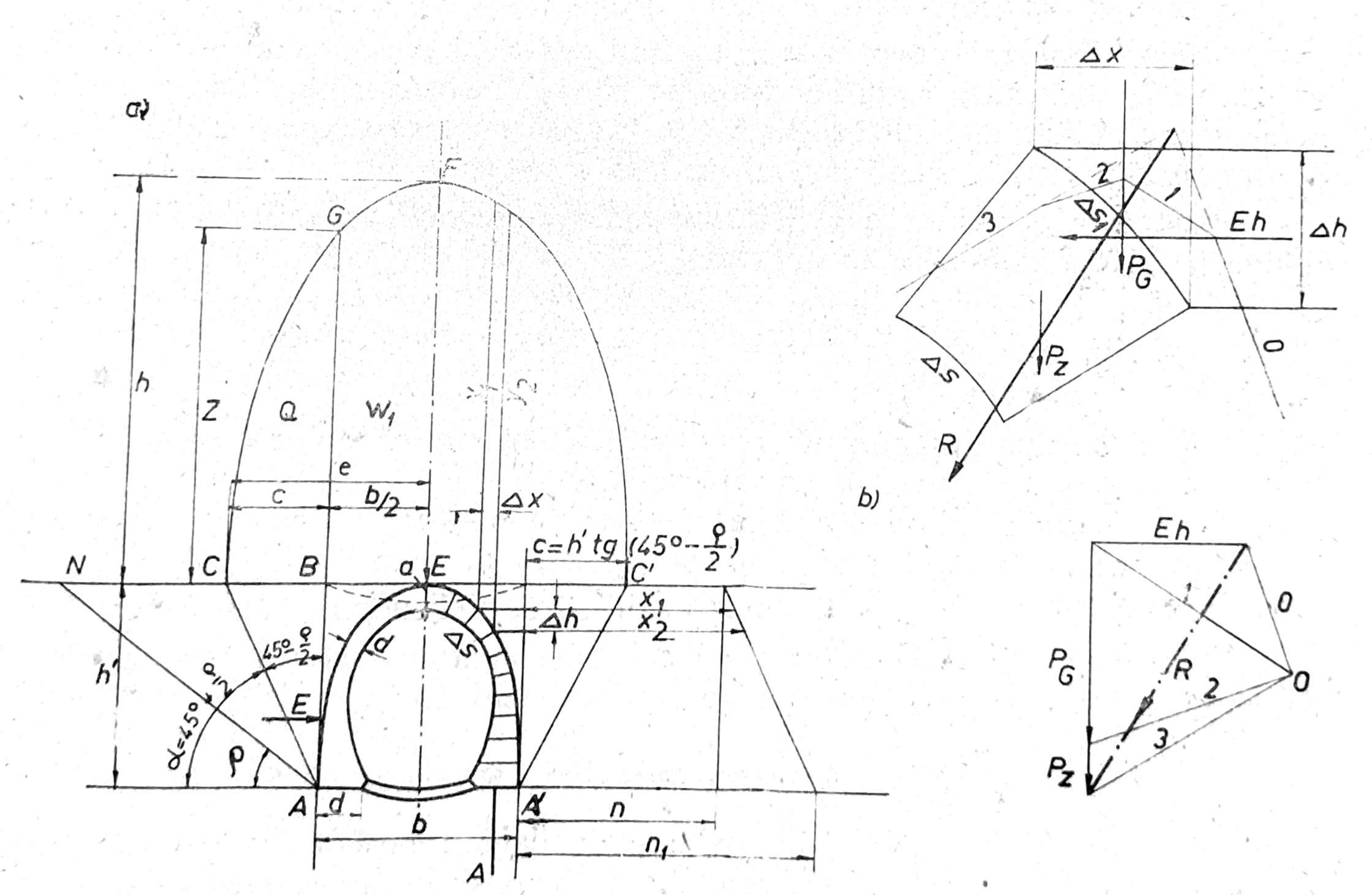
Sl. 7. Određivanje zemljanog pritiska na tunel po Kommerllovoj metodi
Bočni pritisak sastoji se iz zemljanog pritiska Eh, na profil tunela visine h’ i pritiska Ea usled dejstva opterećenja Q
Eh’ = ½ γ h’2 tg2 (45o-ϕ/2); Ea = Q tg(45o-ϕ/2).
Za određivanje bočnih pritisaka Eh na pojedine lamele obloge nanese se dijagram bočnog pritiska (7a) na osnovu jednačina:
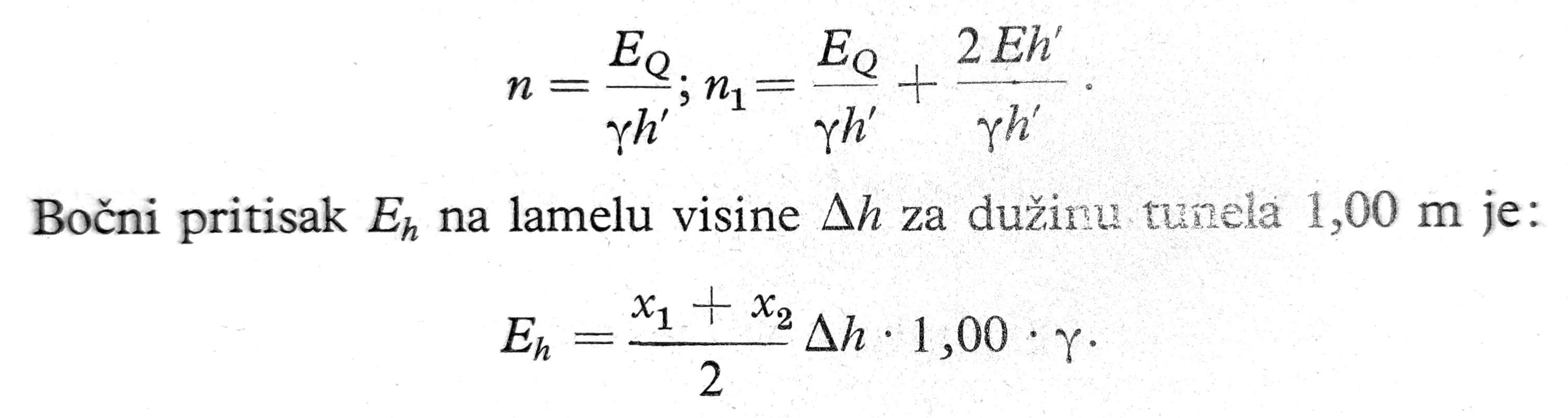
Sile PG i Eh deluju u osovinama odnosnih lamela.
Pored toga odredi se i težina lamele obloge PZ, koja deluje u njenom težištu i nade se rezultanta R svih sila na datu lamelu (sl. 7b). Na taj način odrede se rezultante R1, R2, R3 za sve lamele (sl. 8a), koje se slože u plan sila (sl. 8b), te se dobije rezultanta Rn. Zatim se iz proizvoljnog pola O poruku zraci i nacrta prva potporna linija ac. Iz uslova da je svod u ravnoteži ako se horizontalni pritisak svoda H, rezultanta zemljanog pritiska na tunel Rn i podnožni pritisak A seku u jednoj tački, dobijamo presečnu tačku S. Ako ovu tačku spojimo sa središnom tačkom spojnice svoda u ležištu, dobijamo pravac novog podnožnog pritiska A1. Ako složimo sile Rn, A1 i H u novi plan sila (sl. 8c), dobijamo veličinu H i novi pol O1 iz koga povlačimo nove zrake i drugu potpornu liniju ac’.
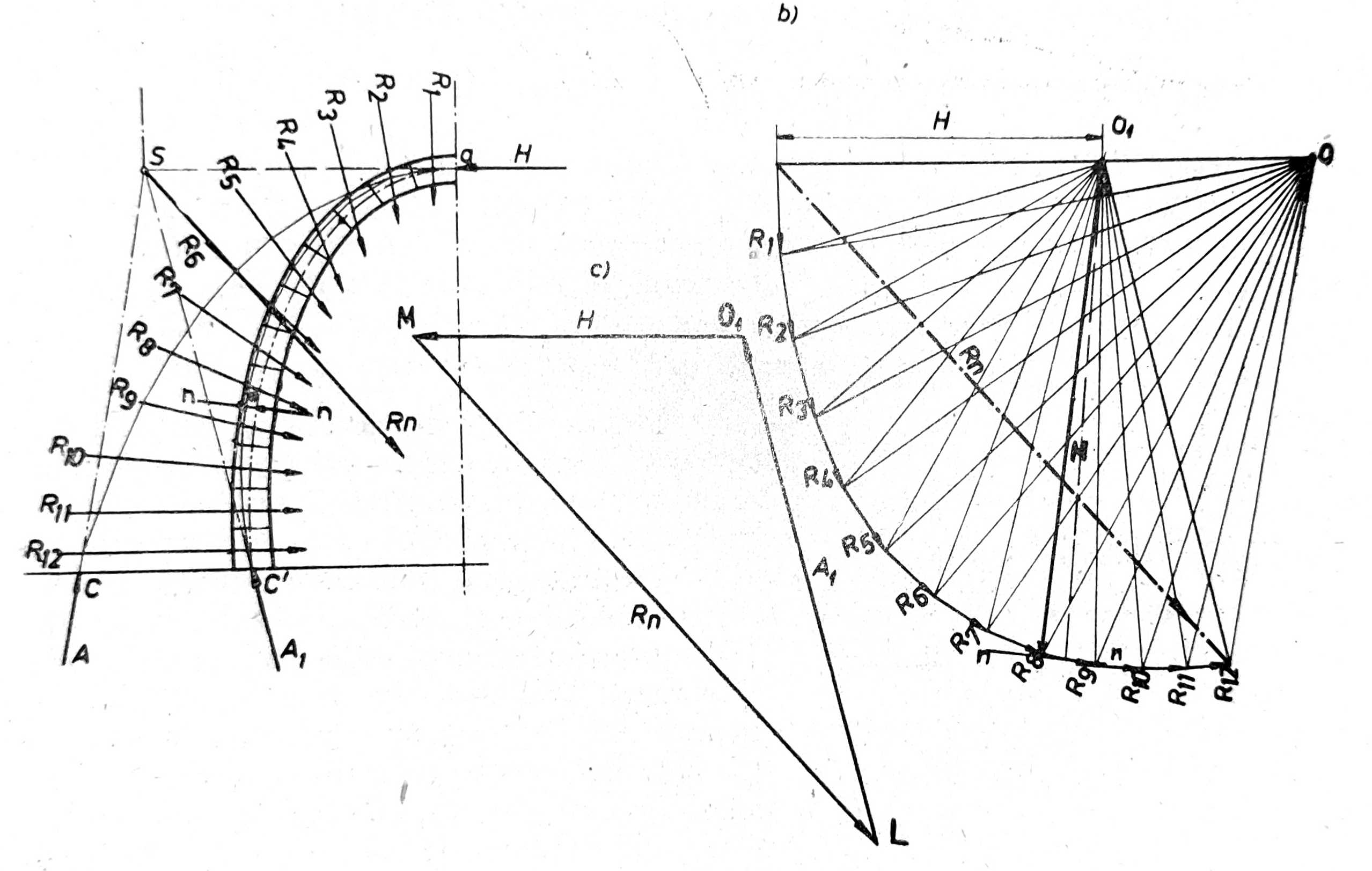
Sl. 8 Plan sila i potporna linija zemljanog pritiska na tunel
Prema dobijenoj novoj potpornoj liniji podešava se poprečni profil tunelske obloge, te se konstruiše potporna linija po potrebi i po treći put. Težnja je da se usvoji takav oblik tunelske obloge, čija se osovina poklapa sa potpornom linijom. U tom slučaju vladaju samo naponi pritiska u oblozi. Napon pritiska koji se javlja u ma kome poprečnom preseku n – n tunelske obloge (sl. 8), dobija se iz obrasca
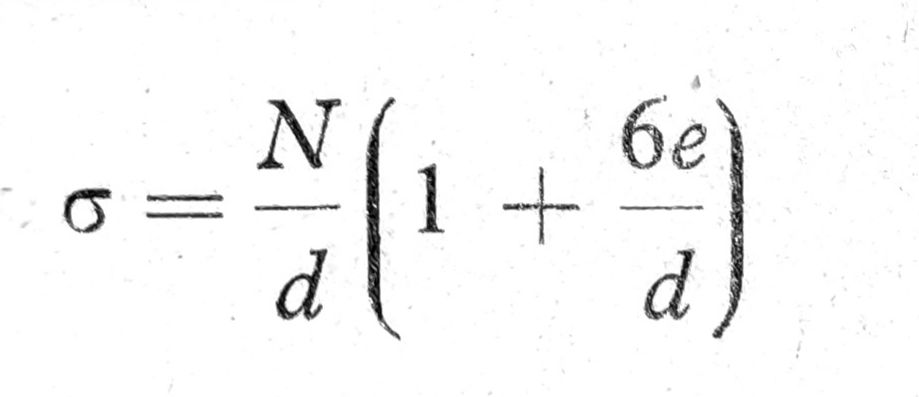
gde je N normalna komponenta rezultante Rn na presek obloge n – n , koje se dobija iz plana sila za taj presek; d debljina tunelske obloge u preseku n – n; e ekscentricitet napadne sile N u istom preseku.
Napon pritiska σ treba da bude manji od dozvoljenog napona obloge. Za tunelske svodove od armiranog betona smatra se da ova metoda nije dovoljno tačna, te se preporučuje Spangerbergova metoda.
