Struktura tla, poroznost i vlažnost

Struktura tla

Pod strukturom tla podrazumeva s raspored čvrste faze u zemljanoj masi. Kao što je poznato, tlo se sastoji iz čvrstih čestica i pora ispunjenih vodom, vazduhom ili vodenom parom, najčešće delimično vazduhom delimično vodom. Prema rasporedu čvrstih čestica u tlu je određena njegova struktura. Strukture nevezanog i vezanog tla se bitno razlikuju među sobom.

Struktura nevezanog tla

Struktura nevezanog tla postaje pod dejstvom gravitacije. Čvrste čestice ovog tla su krupnije i padaju naniže, talože se pod dejstvom gravitacije, dok intermolekularne privlačne sile takvih čestica ne postoje ili su neznatne i savladane gravitacijom. Zbog toga se kod nevezanog tla čvrste čestice slažu jedna pored druge, zauzimajući slobodan prostor između složenih čestica (sl. 1a). Ako su čestice nevezanog tla približno okruglog oblika i iste veličine, kao što može biti slučaj peska ravnomernog sastava, onda struktura može biti najgušća (sl. 1b) ili najređa (sl. 1c), što zavisi od rasporeda čvrstih čestica u tlu. Najgušća struktura odgovara najvećoj mogučnosti zbijenosti nevezanog tla i njegova poroznost je n_min=26%. Najređa struktura odgovara najmanjoj mogućoj zbijenosti nevezanog tla i njegova poroznost je n_max=48%. Tako na primer rastresiti pesak dina ima n=47%.

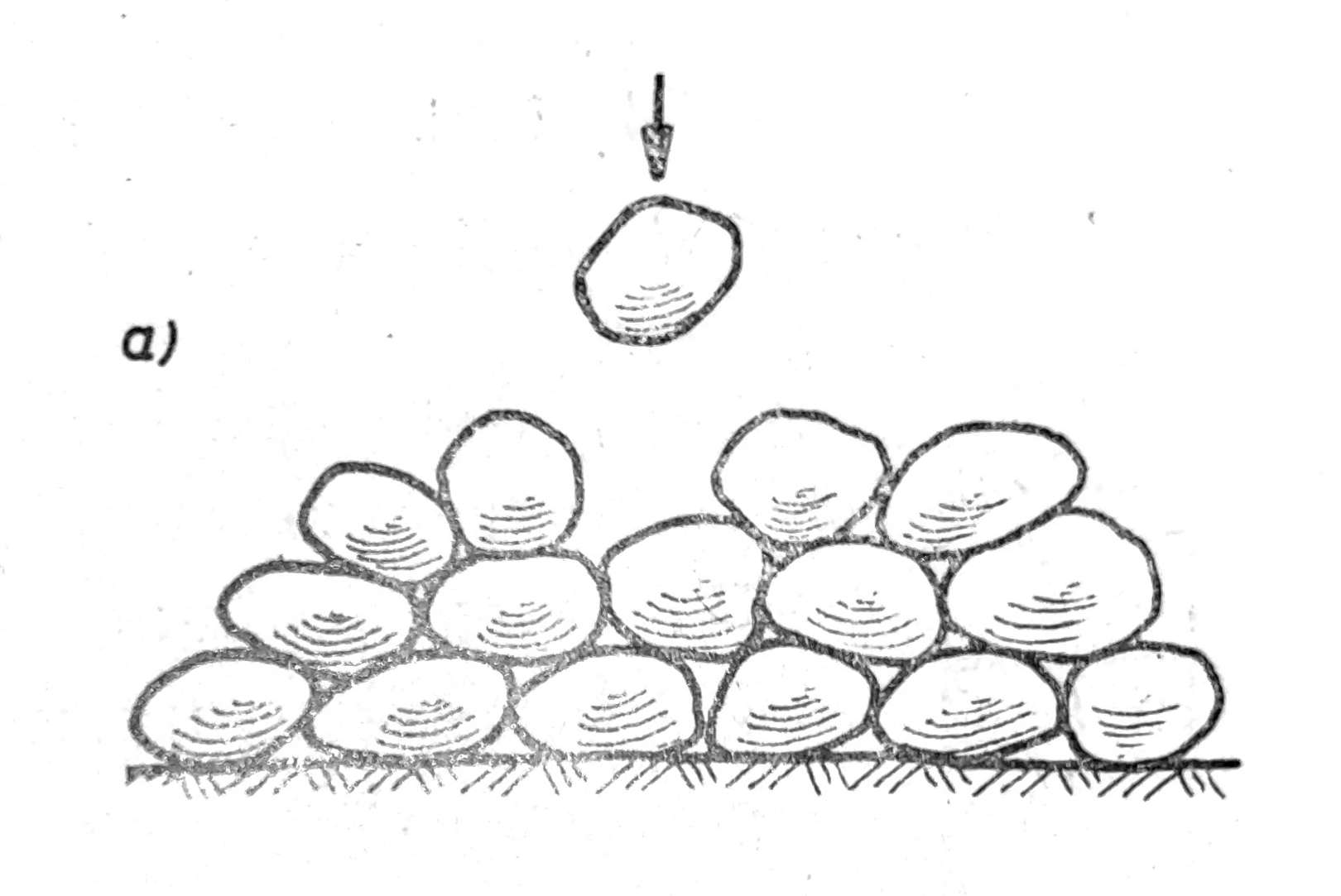
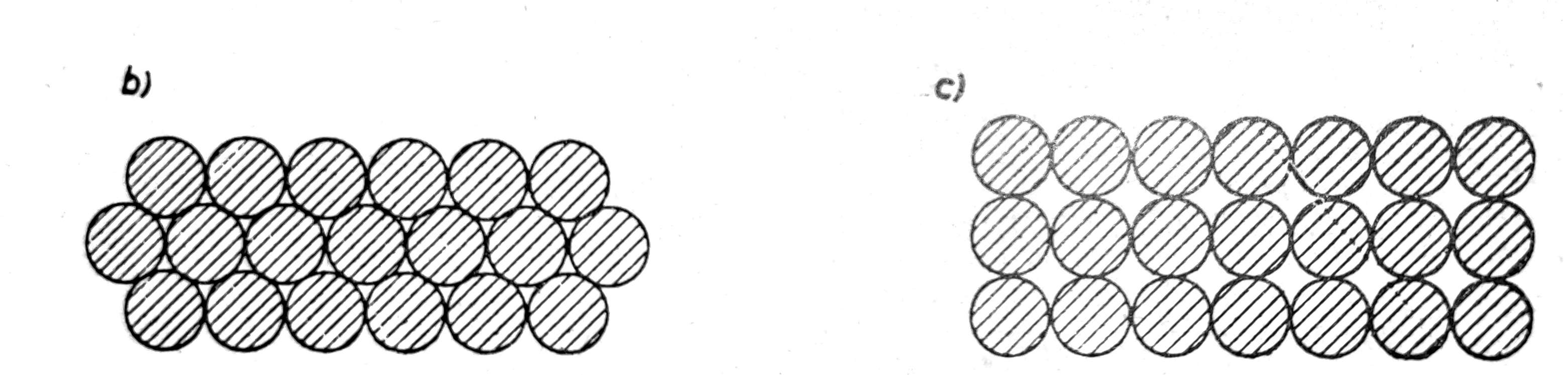
Sl. 1 Struktura nevezanog tla

Ako je nevezano tlo različite krupnoće zrna, tako da sitnije čestice ispunjavaju šupljine između krupnijih (sl. 2), poroznost tla je znatno manja (n=20% i manje).

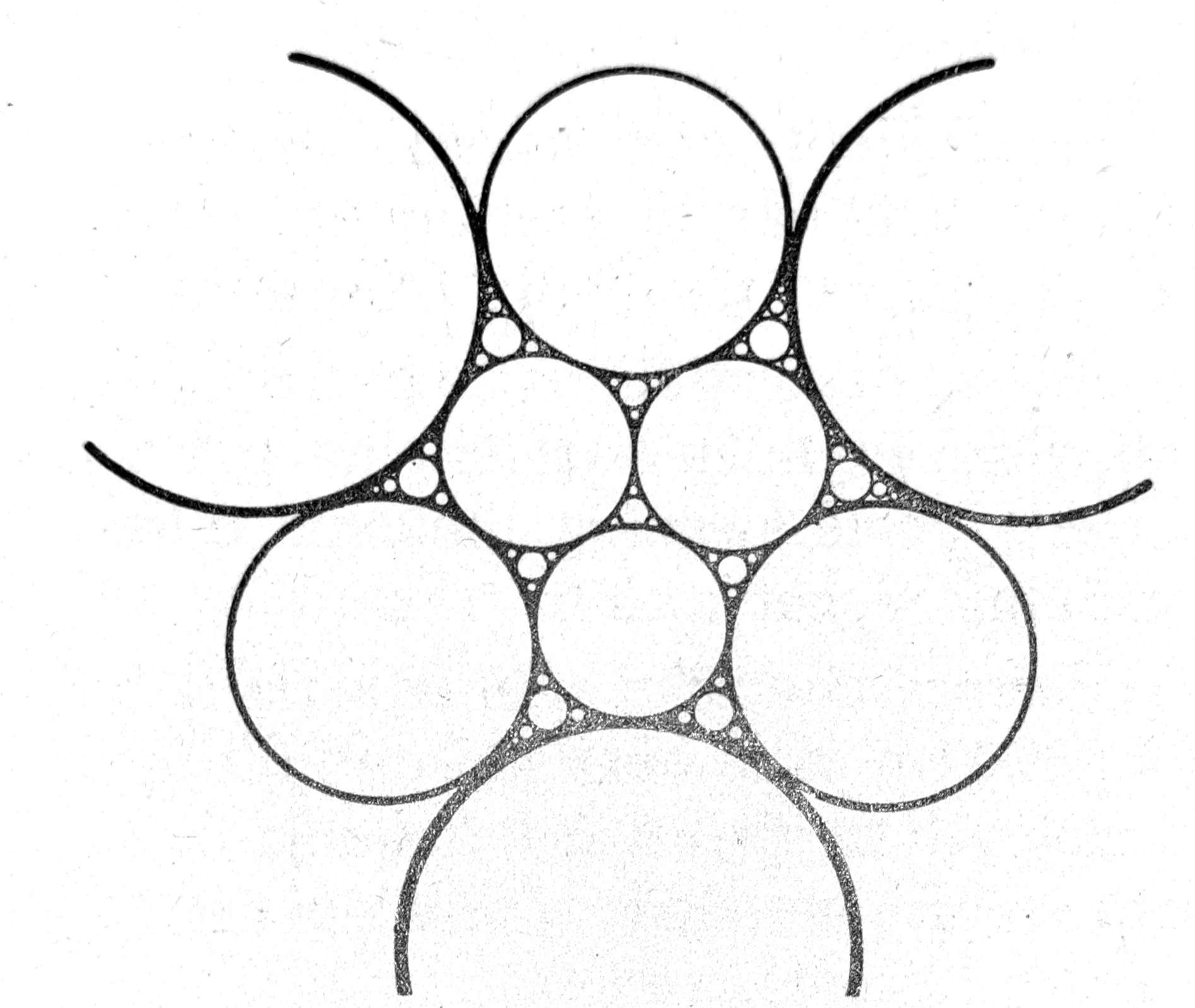
Sl. 2. Struktura nevezanog tla različite krupnoće zrna

Struktura vezanog tla

Kod vezanog tla struktura je drugačija nego kod nevezanog. Kod vezanog tla pojavljuju se sile kohezije, koje su jače od sile gravitacije sitnih čestica i slepljuju ih na dodirnim površinama. Zbog toga ove čestice ne padaju redom naniže, već ostaju slepljene jedna na drugoj i jedna do druge (sl. 3a), stvarajući tako lančano mrežastu strukturu (sl. 3b), pahuljastu (sl. 3c) itd., koje se nazivaju strukture višeg redea. Ovakve strukture imaju veliku poroznost, koja može ići do 60-80% ukupne mase, što ne može biti kod nevezanog tla.

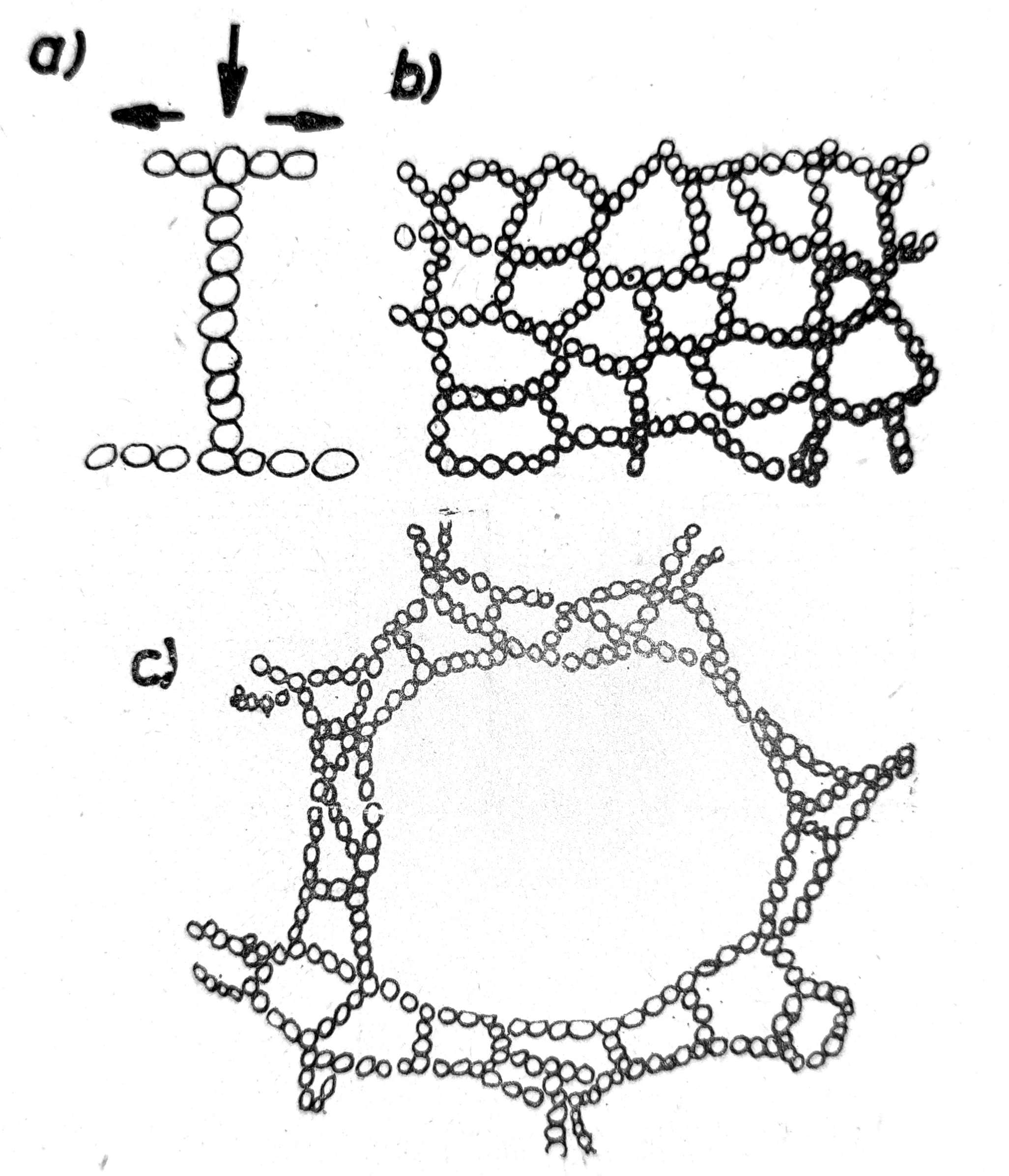
Sl. 3. Struktura vezanog tla

Poroznost i koeficijent poroznosti

Poroznost tla definiše se odnosom zapremine pora prema ukupnoj zapremini tla (sl. 4).

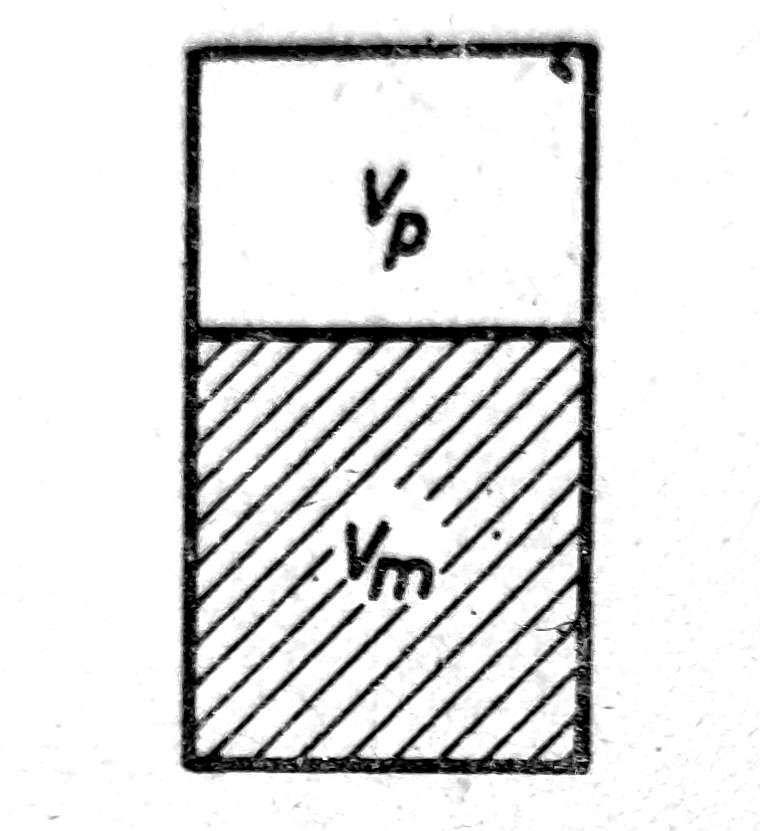
Sl. 4. Poroznost i koeficijent poroznosti tla

Ako označimo sa

• V_p = zapreminu pora u tlu
• V_m = zapreminu čvrstih čestica
• V = ukupnu zapreminu tla,

poroznost tla n je po definiciji

n = V_P / V = V_P / (V_P + V_m),

odnosno u % ukupne zapremine tla

n = 100 * V_P / (V_P + V_m) %.

Koeficijent poroznosti tla definiše se odnosom zapremine pora prema zapremini čvrstih čestica:

e = V_P / V_m.

Iz obrasca za poroznost n imamo:

nV_P + nV_m = V_P, odakle je V_m = V_P(1-n) / n.

Zamenjujući ovu vrednost u obrascu za e dobijamo

e = n / (1-n).

Iz ove jednačine dobijamo

e – n e = n  i  n = e / (1+e).

Koeficijent poroznosti pokazuje gustinu tla. Ukoliko je koeficijent e veći, utoliko je gustina tla manja i obrnuto. Ako se neko stišljivo tlo pod opterećenjem sleže, pomoću koeficijenta poroznosti pre i posle sleganja može se odrediti veličina sleganja Δh.

Posmatrajmo sloj stišljivog tla debljine h (sl. 5a). Ako ovaj sloj opteretimo, on će se slegnuti za visinu Δh, tako da će se njegova debljina usled opterećenja smanjiti na h₁. Prema tome

Δh = h – h₁.

Pošto se sleganje stišljivog tla vrši na račun pora, jer su čvrste čestice praktično nestišljive, a takođe i voda, ako su pore tla njome ispunjene delimično ili potpuno, to se ovo sleganje može predstaviti šematski na sl. 5b.

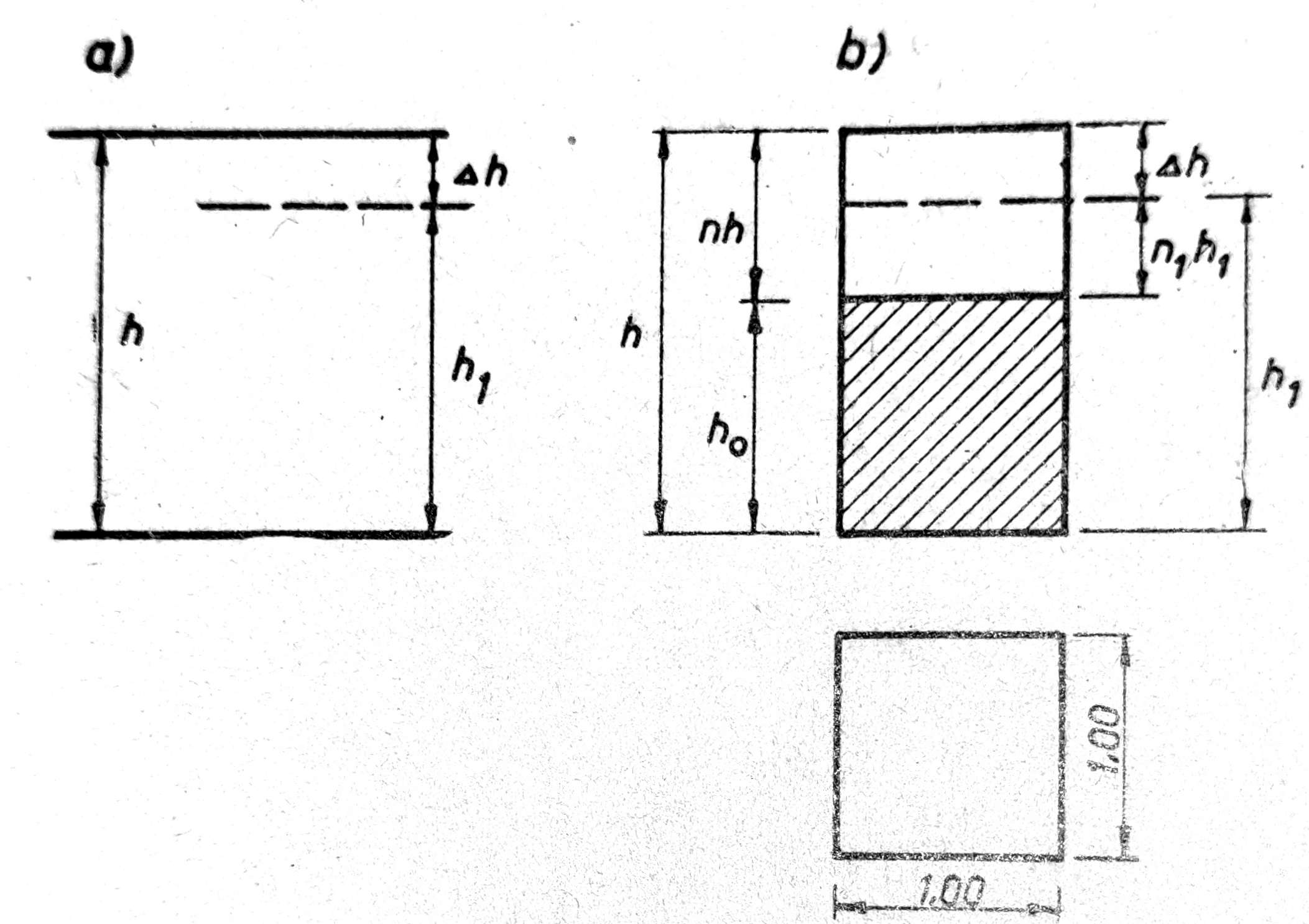
Sl. 5. Sleganje Δh stišljivog sloja tla debljine h pod opterećenjem

Ako označimo sa h₀ zamišljenu visinu sloja čvrstih čestica bez pora, zvanu redukovana visina, onda možemo izraziti sleganje Δh u odnosu na redukovanu visinu h₀ odnosom:

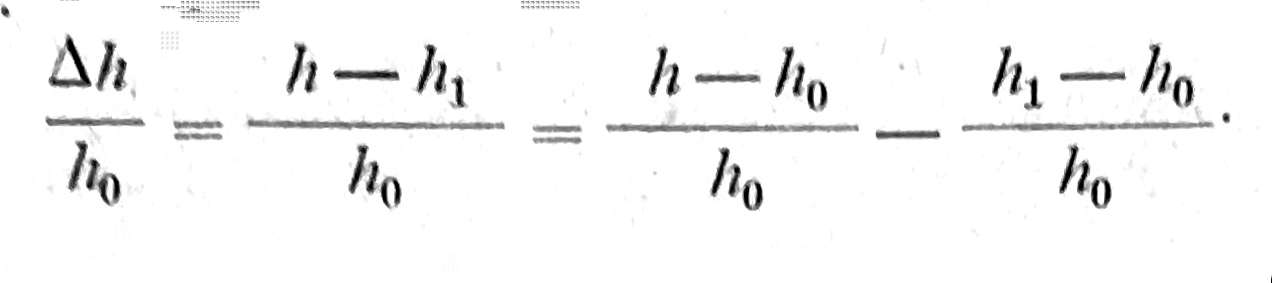
Ako posmatramo sloj tla širine i dužine koje su jednake jedinici, onda visine h, h₁ i h₀ predstavljaju zapremine, te je

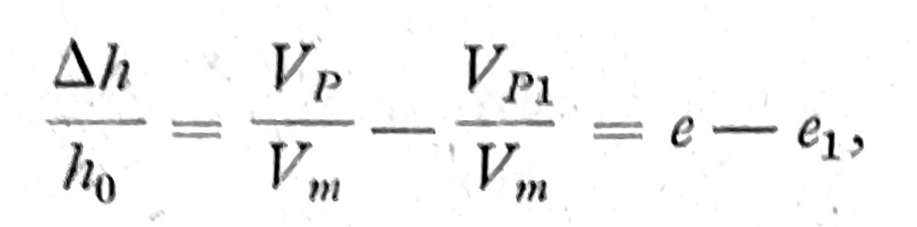
gde je e koeficijent poroznosti pre, e₁ posle sleganje. Iz prednjeg dobije se sleganje

Δh = h₀ (e-e₁).

Sleganje se može izraziti u odnosu na visinu sloja h pre sleganja ako zamenimo vrednost redukovane visine h₀:

h₀ = h – nh = h (1-n) = h / (1+e),

pošto je n = V_P / V = V_P / h, odakle je V_P = nh.

Prema tome se dobije

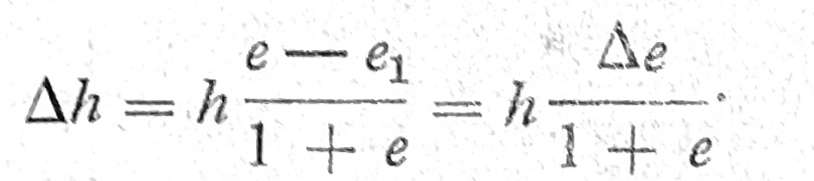
Pojedine vrste tla imaju sledeće prosečne vrednosti poroznosti n i koeficijenta poroznosti e:

Vlažnost tla

Vrste vode u tlu

Voda u tlu pojavljuje se u obliku vode u porama između čvrstih čestica tzv. porna voda, zatim kao adsorbovana voda na čvrstim česticama i kao konstituciona voda.

Porna voda sastoji se iz slobodne vode između čvrstih čestica, čije kretanje se vrši po Darcy-evom zakonu, zatim gravitacione vode, koja se kreće pod dejstvom gravitacije odozgo naniže u svim pravcima, ali se njeno kretanje ne vrši po Darcy-evom zakonu, kapilarne vode koja se kreće pod dejstvom kapilarnih sila i vode površinskog napona, koja se drži površinskim naponom u uglovima između čvrstih čestica tla i naziva se još ugaona porna voda. Sva ova voda može se potpuno ukloniti sušenjem tla na temperaturi od 110^oC.

Adsorbovana voda je ona koja obavija čvrste čestice, za koje je vezana molekularnim silama. To je tzv. vodeni film, čija debljina se kreće 6-80 µµ (1µµ=10^-6 mm, milimikron). Uticaj adsorbovane vode kod krupnijih čestica je neznatan, međutim ukoliko su čestice sitnije utoliko je njen uticaj veći, jer se povećava opšta površina čestica a time i odnos adsorbovane vode prema čvrstim česticama u jedinici zapremine tla. Ova voda može se samo delimično ukloniti sušenjem na 110^oC.

Konstituciona voda je hemijski sjedinjena u kristale minerala čvrstih čestica tla. Ove vode ima vrlo malo i ona se ne može ukloniti sušenjem tla. Stoga se ova voda može smatrati kao sastavni deo čvrste čestice.

Količina vode u tlu

Po definiciji količina vode u tlu ili vlažnost tla je odnos težine vode sadržane u tlu prema težini njegovih čvrstih sastojaka. Prema količinik vode u tlu razlikuju se tri slučaja: tlo potpuno zesićeno vodom, tlo delimično zasićeno vodom i tlo potpuno suvo.

Tlo potpuno zasićeno vodom

Ako označimo sa n poroznost tla, γ_s zapreminsku težinu svih čestica, γ_w zapreminsku težinu vode, onda se vlažnost zasićenog tla w_Z može izraziti sledećom jednačinom

Tlo delimično zasićeno vodom

Ako označimo sa W_w težinu vode sadržane u tlu, sa W_d  težinu čvrstih čestica odnosno suvu težinu tla, onda je vlažnost tla w

w = W_w / W_d , odnosno u procentima suve težine tla: w = 100 W_w / W_d.

U ovom slučaju vlažnost tla se može izraziti stepenom vlažnosti S_r koji predstavlja odnos stvarne težine vode u tlu prema onoj težini vode u istom tlu koja bi kada bi sve pore bile ispunjene vodom, odn. prema težini vode zasićenog tla:

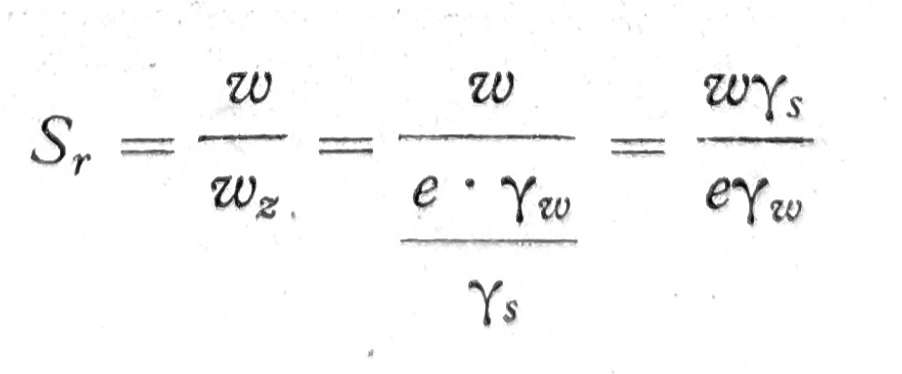
odn. za γ_w = 1,00  S_r = w*γ_s / e.

Granične vrednosti za stepen vlažnosti su:

1. za potpuno suvo tlo w = 0; S_r = 0
2. za potpuno zasićeno tlo w = e/γ_s; S_r = e/γ_s * γ_s / e = 1,0.

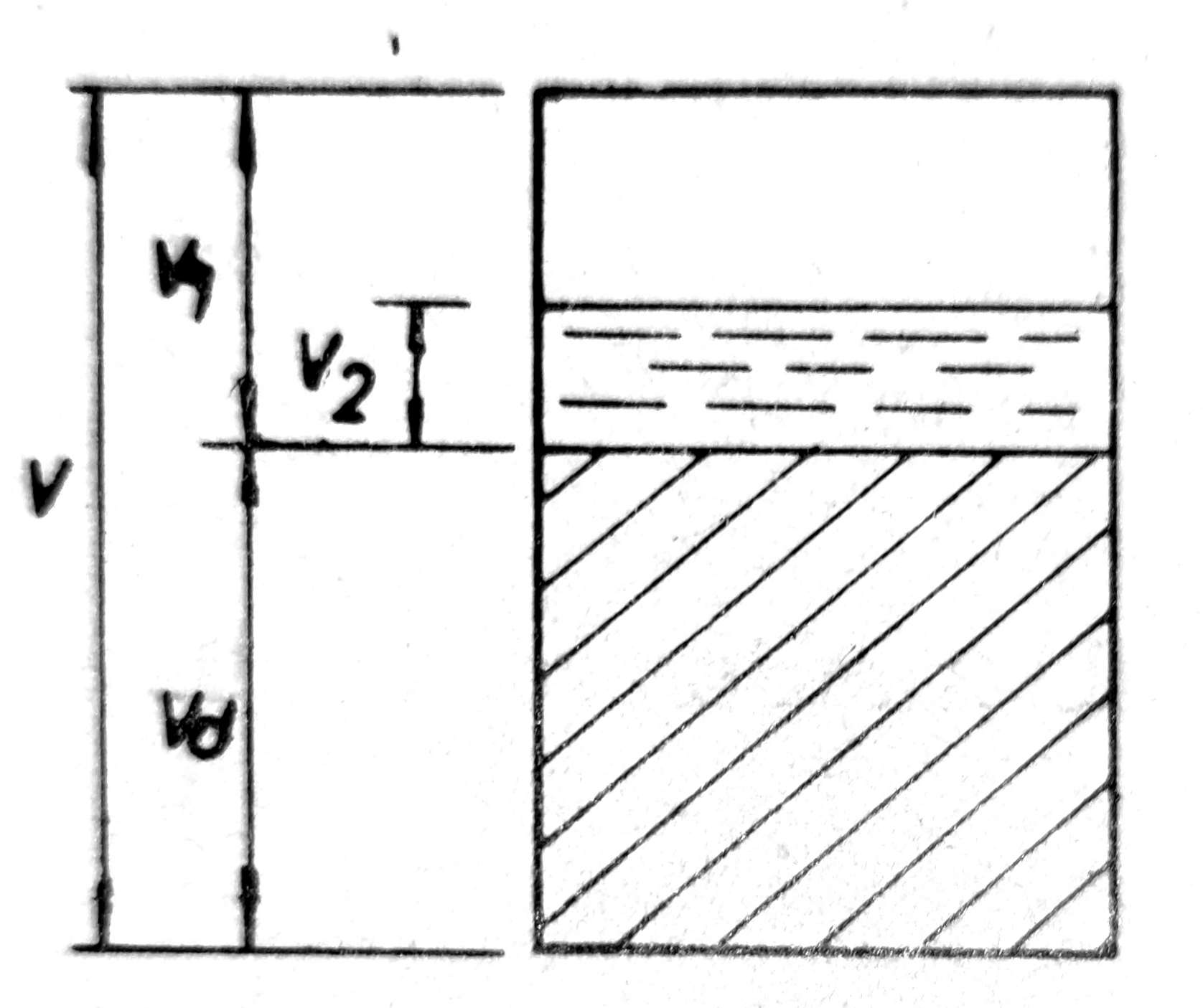
Sl. 6. Uzorak tla delimično zasićen vodom

Stepen zasićenja (koji se ponekad naziva takođe zasićenost ili stepen vlažnosti) izražava se još i odnosom zapremine pora ispunjenih vodom prema ukupnoj zapremini pora (sl. 6):

S_r = V₂ / V₁

gde je V₂ zapremina pora ispunjenih vodom, V₁ ukupna zapremina pora ispunjenih vodom, vazduhom i gasovima. Ako je w vlažnost tla u % suve težine tla W_d, onda imamo

V₂ * γ_W = w W_d, odakle je V₂ = w W_d / γ_w.

S druge strane, imamo da je V₁ = V – V_d, pa kako je V_d * γ_s = W_d, to je

V_d = W_d / γ_s i V₁ = V – W_d / γ_s.

Prema tome, stepen zasićenja tla S_r biće

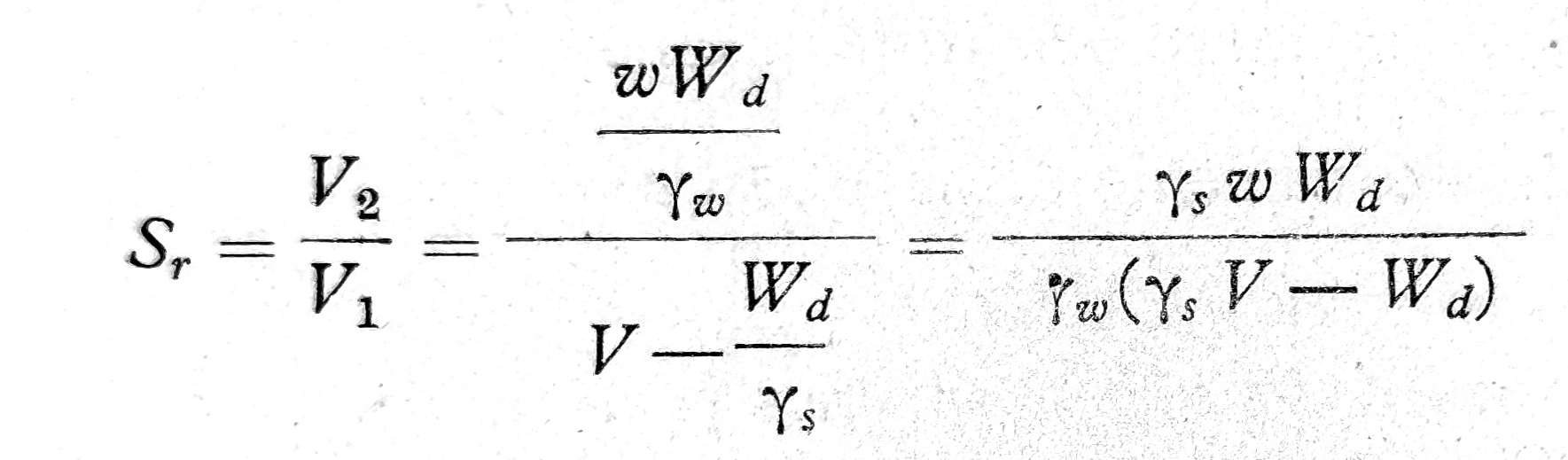
odnosno u procentima suve težine tla

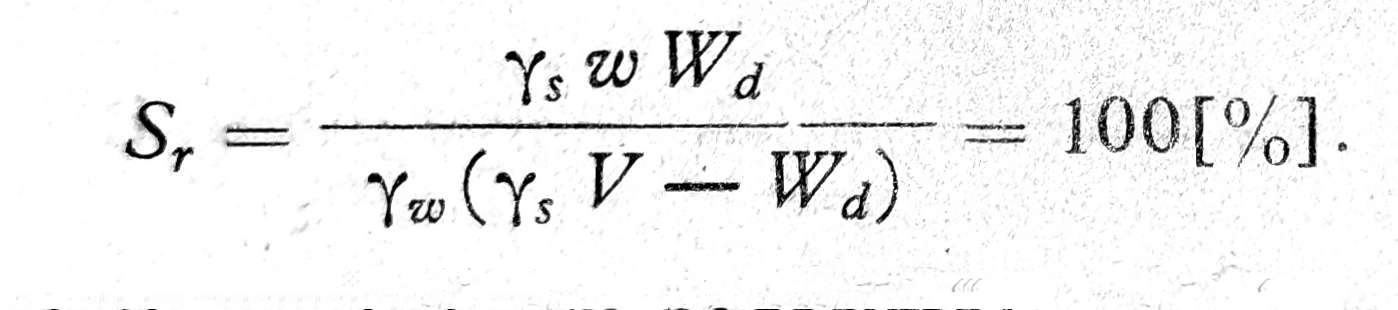
Tlo potpuno suvo

U ovom slučaju je w = 0. Sva porna voda je uklonjena, dok je adsorbovana voda samo delimično uklonjena, tj. vodeni film i dalje postoji, ali je njegova debljina smanjena.