Pod dejstvom opterećenja svako tlo, sa izuzetkom čvrste stene, sleže se. Sleganje uopšte nastaje iz dva uzroka: zbijanja tla tj. smanjenja njegove zapremine usled isterivanja vazduha ili vode iz njegovih pora i bočnog istiskivanja tla pored ivica temelja usled klizanja čvrstih čestica tla.
Sleganje tla usled zbijanja sastoji se iz elastičnih i plastičnih deformacija, prouzrokovanih opterećenjem temelja, kod kojih se pri rasterećenju tlo vraća delimično u prvobitno stanje.
Sleganje usled bočnog istiskivanja tla sastoji se samo iz plastičnih deformacija, kod kojih se pri rasterećenju tlo ne vraća u prvobitno stanje. Ona nastaju najčešće kod malih temelja izrađenih na maloj dubini ispod površine terena. Isto tako do bočnog istiskivanja tla dolazi kod jako vlažnog tla i čiji ugao unutrašnjeg trenja je mali.
S obzirom da se dozvoljeno opterećenje tla uzima u zoni elastično plastičnih deformacija, proračun sleganja vrši se samo na bazi smanjenja poroznosti tla pod opterećenjem, pri čemu se zanemaruju sleganja usled bočnog istiskivanja tla, koja se usvajaju da su neznatna.
Sleganje usled zbijanja zavisi od propustljivcsti tla, pošto se ono vrši na račun pora, koje su u prirodnom tlu uvek manje ili više ispunjene vodom. Prema tome, sleganje tla pod opterećenjem je ustvari hidrodinamička pojava, jer proces sleganja zavisi od brzine istiskivanja vode iz pora, u kome propustljivost tla ima najveću ulogu.
Nekoherentna tla kao što su šljunak i pesak imaju velike pore, zbog čega je njihova propustljivost velika i voda iz pora pod opterećenjem temelja brzo se istiskuje. Stoga se kod nekoherentnog tla sleganje pod opterećenjem temelja brzo obavlja, najčešće još za vreme građenja ili kratko vreme iza toga. Zbog toga se retko izračunava sleganje temelja u nekoherentnom tlu.
Koherentna tla imaju sitne pore, njihova propustljivost je mala i istiskivanje vode iz pora pod dejstvom opterećenja temelja može da traje vrlo dugo, kod nekih sitnozrnih glina i decenijama. Osim toga, pošto je ukupna poroznost koherentnog tla znatno veća nego nekoherentnog, sleganje koherentnog tla je mnogo veće.
Kod koherentnog tla, čije pore su delimično ispunjene vazduhom a delimično vodom, nastaje najpre sleganje usled zbijanja vazduha u porama, dok sadržina vode ostaje konstantna, a zatim sleganje usled istiskivanja vode iz pora. Pri statičkom opterećenju tla usled dejstva težine i korisnog opterećenja temelja nastaju obe ove vrste sleganja, ali je vremenski proces sleganja različit.
Postoje i drugi uzroci koji izazivaju sleganje tla, kao što su trajno spuštanje nivoa podzemne vode, hemijske promene sastava tla i drugi poremećaji u tlu.
Proučavanje sleganja sastoji se iz prethodnog proračuna sleganja, koji se radi na osnovu laboratorijskog ispitivanja uzoraka tla i osmatranja sleganja, koje se vrši za vreme građenja objekta i određeno vreme posle toga.
Proračun sleganja kod centričnog opterećenja temelja
Posmatrajmo temeljnu stopu fundiranu u tlu koje se sastoji iz više različitih slojeva, na primer sloja peska H0, odnosno H1 ispod stope, sloja glinovitog tla debljine H2, sloja sitnozrne gline debljine H3, ispod koga je zbijen šljunak veće debljine sloja, sa nivoom podzemne vode NPV (sl. 1a).
Za proračun sleganja potrebno je naneti dijagram napona usled sopstvene težine tla (levi dijagram na sl. 1b) i dijagram napona usled dejstva dopunskog opterećenja od temelja (desni dijagram na sl. 1b). Dijagram napona usled sopstvene težine tla dobijamo iz debljine slojeva ΣH i njihovih zapreminskih težina γ. Ako je zapreminska težina peska γ1, peska pod vodom γ’1, glinovitog tla pod vodom γ’2, gline pod vodom γ’3, naponi pritiska u tlu od sopstvene težine tla biće (sl. 1)
γ1 · H’; γ’1 · H’’; γ’2 · H2; γ’3 · H3;
Dijagram napona usled dejstva opterećenja dobijamo proračunom po nekoj od poznatih metoda, na primer po Steinbrenneru ili Newmarku, za različite dubine ispod temelja.
Ako označimo sa P opterećenje temelja, A njegovu površinu kojom naleže na tlo, γ1 zapreminsku težinu tla u dubini fundiranja t ispod površine terena, specifično opterećenje temelja je P/A dok je sopstvena težina tla na istoj dubini γ1t. Da bi se dobilo dopunsko opterećenje tla usled opterećenja temelja, treba oduzeti pritisak sopstvene težine tla γ1t od opterećenja temelja P/A, tako da dopunsko opterećenje tla iznosi
p0 = P/A – γ1t.
Na istoj dubini t deluje i napon γ1t usled sopstvene težine tla, tako da na ovoj dubini deluje ukupan napon (P/A – γ1t) + γ1t, pri čemu je konsolidacija tla pod naponom γ1t izvršena pre građenja objekta.
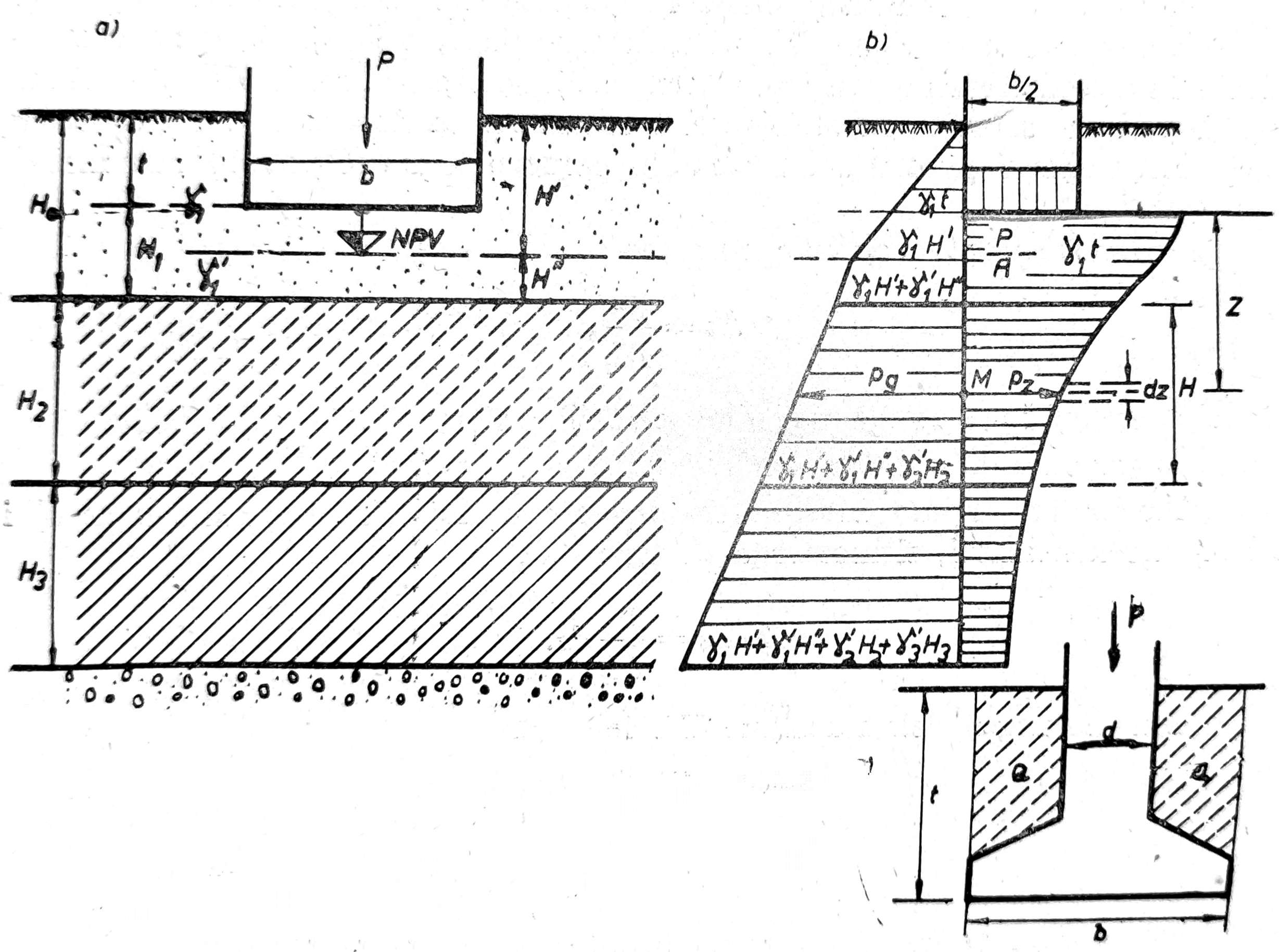
Sl. 1. Proračun sleganja kod centričnog opterećenja temelja
Međutim ako se jedan deo temelja iznad temeljne stope zatrpava zemljom (sl. 1c), treba uzeti u obzir opterećenje nasutog tla 2Q, tako da u tom slučaju dopunsko opterećenje iznosi
P+2Q/A – γ1t.
Za temelj oblika trake je A = b x 1,0 m na 1 m' temelja.
Proračun sleganja radi se za sve slojeve stišljivog tla do dubine dejstva opterećenja temelja. Ranije se smatralo kao granica dejstva opterećenja objekta dubina do koje vladaju naponi intenziteta ≥ 10% p0. Danas se usvaja da je ova granica na dubini gde je napon od dopunskog opterećenja pz jednak 20% napona od sopstvene težine tla: pz = 0,2 ·γΣH. Ispod ove dubine ne računa se sleganje. Prema jednom drugom pravilu se preporučuje proračun sleganja za slojeve do dubine 2b do 3b, pri čemu je b širina temelja. Ako se na kraju nalazi šljunčani sloj kao na sl. 1a, on se ne uzima u obzir za proračun sleganja, jer je njegovo sleganje pod opterećenjem temelja neznatno i obavlja se za vreme građenja.
U dubini z ispod temeljne stope postoji napon pritiska pg usled sopstvene težine tla (sl. 1b), pri čemu je uzet u obzir i uticaj uzgona. Ovom početnom naponu pritiska dodaje se pritisak pz usled dejstva opterećenja objekta na istoj dubini. Prema tome, u nekoj ma kojoj tački M na dubini z ispod temeljne stope vlada ukupan napon pritiska pn = pg + pz.
Pod dejstvom dopunskog opterećenja, tlo se sleže i bočno deformiše. Ako se bočne deformacije zanemare, jer su srazmerno male, pošto je dozvoljeno opterećenje tla u zoni elastično plastičnih deformacija, može se usvojiti da se proračun sleganja vrši na osnovu opita stišljivosti u edometru, sa neporemećenim uzorkom izvađenim u oblasti posmatrane tačke u tlu, pomoću koga opita se određuje modul stišljivosti tla Ms.
Na osnovu Hookeovog zakona imamo
Δs = pz/Ms,
gde je Δs specifično sleganje, na jedinicu debljine sloja, pz napon u dubini tla z usled dopunskog opterećenja.
Ako predpostavimo dovoljno malu debljinu sloja dz, da se mogu usvojiti pz i Ms kao konstantni, elementarno sleganje biće
Δs dz = pz/Ms dz.
Ukupno sleganje sloja debljine H biće
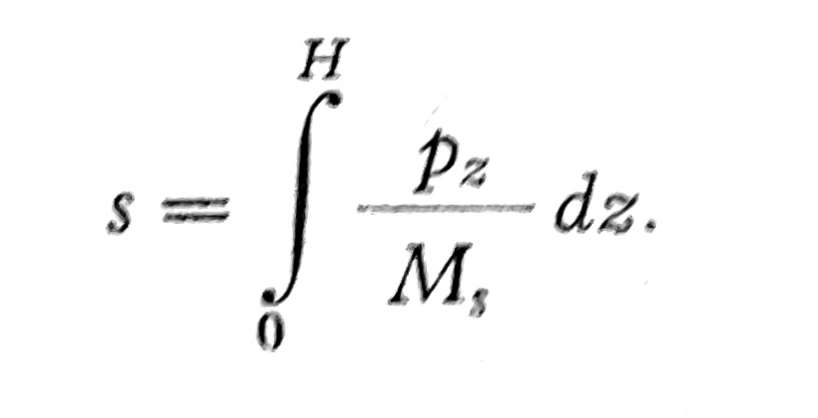
Ako su pZ i MS konstantni za sloj debljine H, biće
s = pz/Ms · H.
Ustvari pz i Ms nisu konstantni za sloj debljine H1, već se usvaja njihova srednja vrednost u tački M.
Modul stišljivosti tla Ms određuje se laboratorijskim putem za svaki sloj zasebno. Za normalno konsolidovano tlo, modul Ms odreduje se iz dijagrama primarne kompresije, gde je ukupno opterećenje σ2 = pg + pz; σ1 = pg = Σγt, dopunsko opterećenje Δσ = σ2 – σ1 = (pg + pz) – pg, a odgovarajuće vrednosti relativne kompresije su Δh2/h i Δh1/h, te je
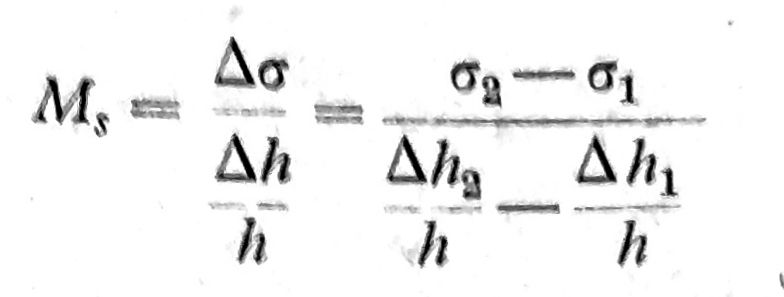
Međutim ako je u pitanju prekonsolidovana glina, onda se modul stišljivosti određuje iz dijagrama sekundarne kompresije. Iz primera na sl. 2 imamo za:
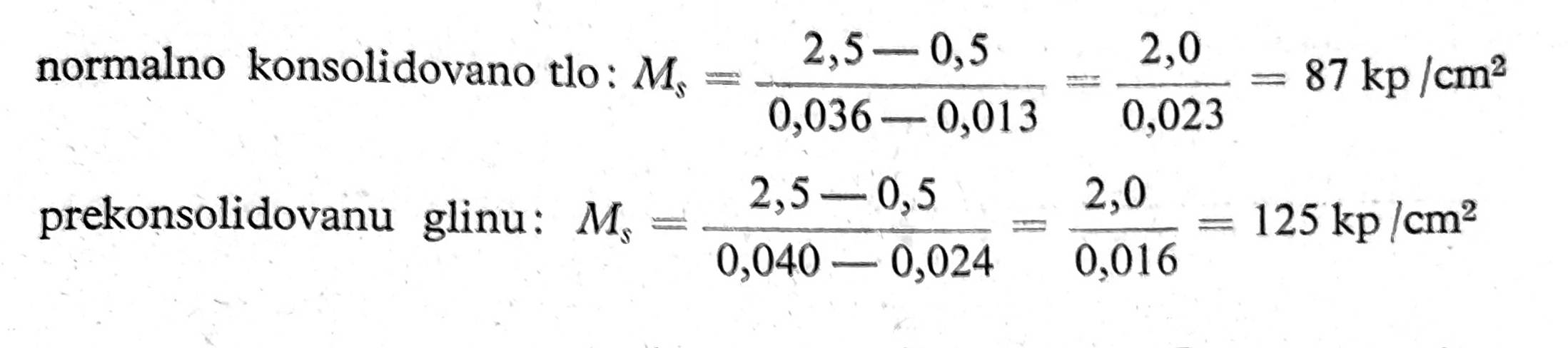
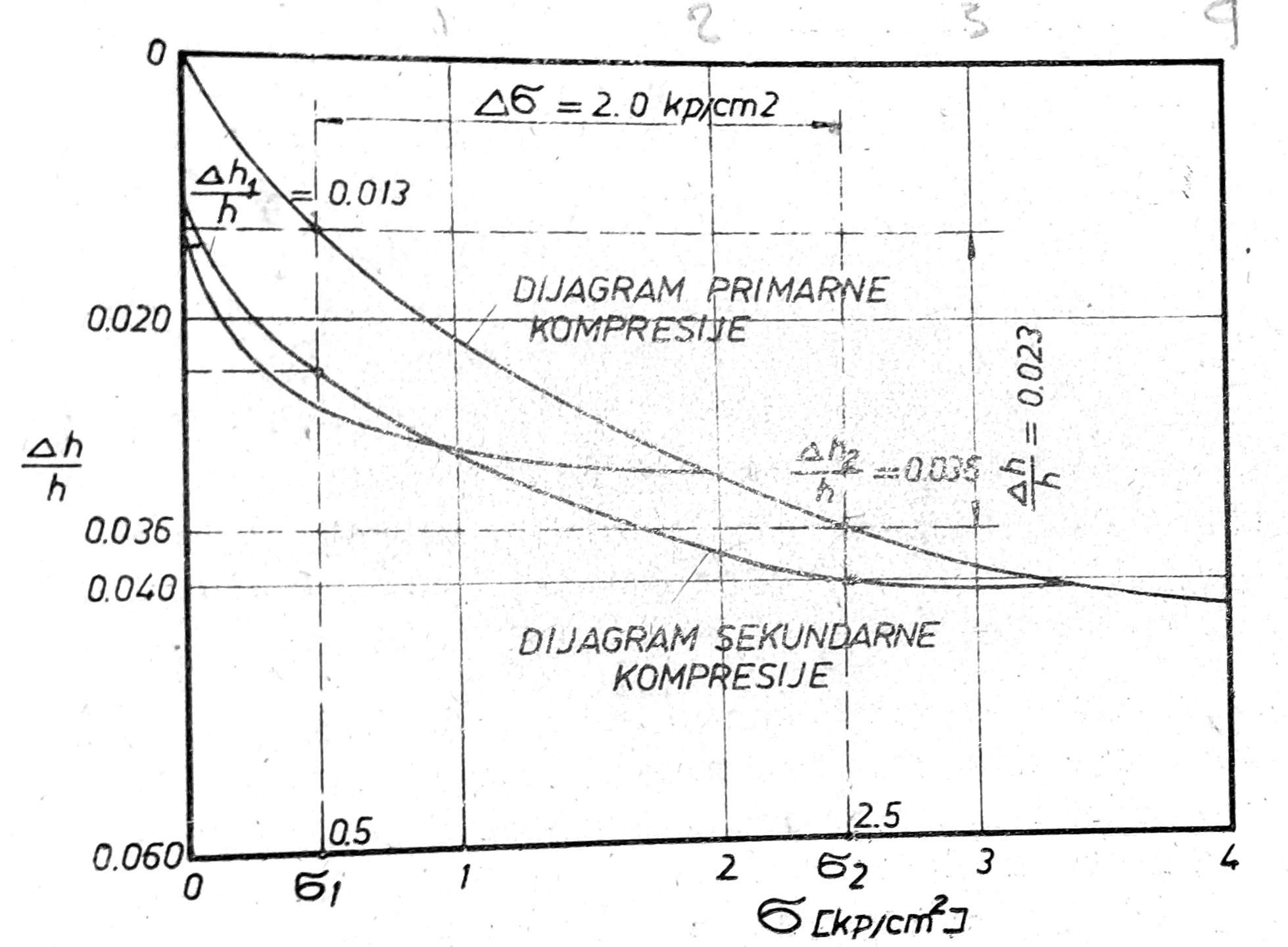
Sl. 2. Određivanje modula stišljivosti tla na osnovu dijagrama relativne kompresije
Iz prednjeg proizlazi da će sleganje prekonsolidovane gline biti mnogo manje od sleganja normalno konsolidovanog tla.
Uticaj krutosti temelja na sleganje
Mada praktično ne postoje potpuno elastični temelji, kod kojih bi sleganje jedne tačke bilo nezavisno od sleganja susedne tačke, za proračun sleganja razlikuju se elastični i kruti temelji.
Elastični temelji, pod kojima se podrazumevaju kameni nabačaji i nasipi, pri ravnomernom opterećenju prouzrukuju u pojedinim tačkama različita sleganja. Zbog toga se kod ovih temelja proračun sleganja ne vrši za celu opterećenu površinu, već za pojedine njene tačke: ugaone tačke A, B, C i D srednje tačke strana E, F, H i J i središne tačke G površine pravougaonika (sl. 3). Kod ravnomernog opterećenja sleganje tačaka B, C i D je isto kao i tač. A, sleganje tačke, H je isto kao i tačke E, tač. J isto kao tač. F za tlo istog sastava.
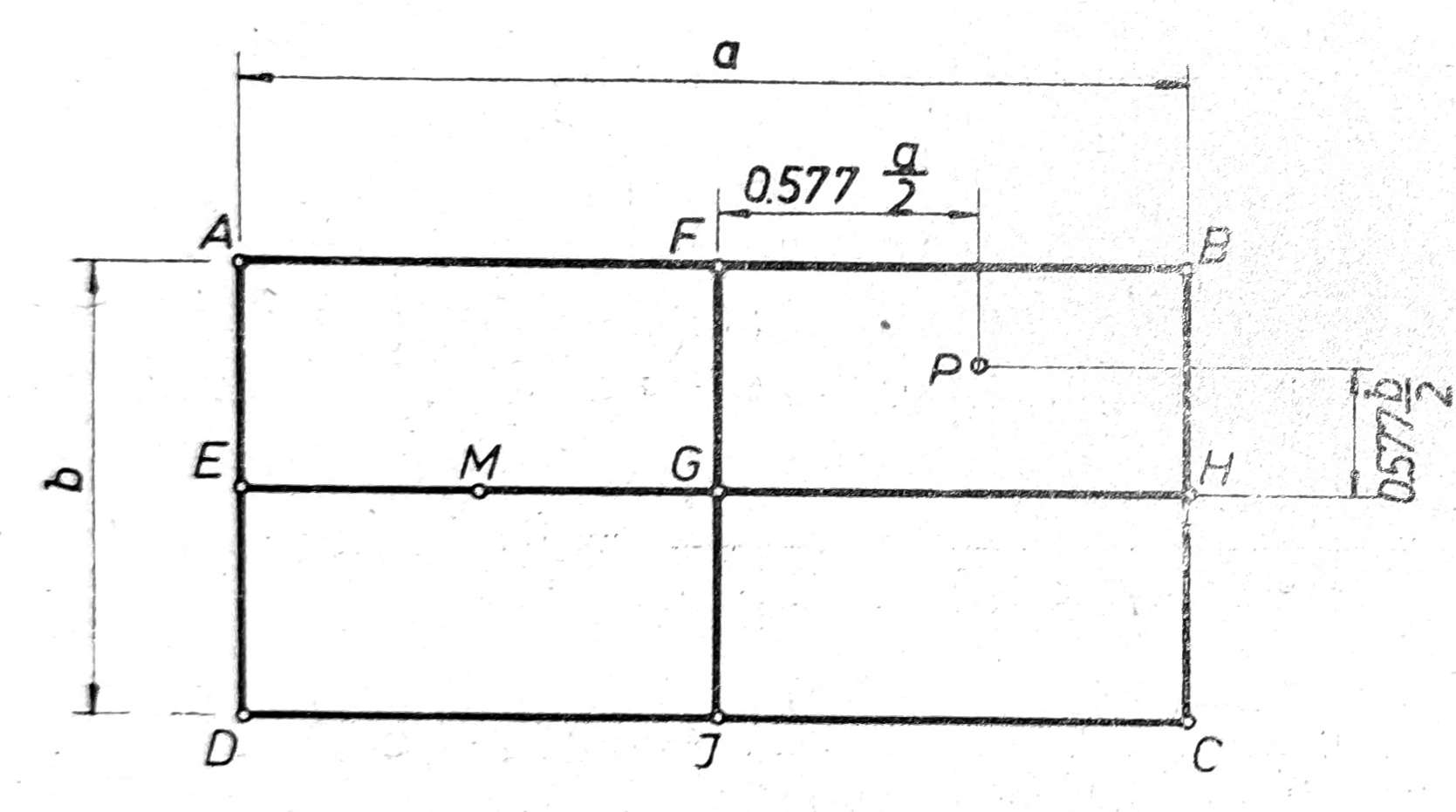
Sl. 3. Proračun sleganja pojedinih tačaka opterećene površine
Za izračunavanje sleganja ispod jedne makoje tačke G opterećene površine, podeli se pavougaonik ABCD na četiri manja pravougaonika i sleganje G dobija se kao zbir sleganja koja prouzrukuje svaki od podeljenih pravougaonika.
Kruti temelji ne sležu se na isti način kao elastični, pošto kod njih nije moguće sleganje pojedinih tačaka. Stoga se sleganje krutih temelja računa kao celina s tim, što se prema stepenu krutosti izračunava srednja vrednost sleganja na različit način, pošto od krutosti temelja zavisi raspodela pritiska u temeljnom dnu.
Za krute temelje oblika kvadrata ili manjeg pravougaonika, kod kojih je a < 2b, izračuna se sleganie sG srednje tačke G i usvaja opšte sleganje temelja s = 3/4 sG. Za krute temelje oblika izduženog pravougaonika ili trake izračunava se sleganje krajnje tačke E, srednje tačke G i tačke M na polovini odstojanja između njih, po dužoj osovini temeljne stope, te se usvaja srednja vrednost.
Van Hamme smatra da je tačniji proračun sleganja „karakteristične tačke P“, koja se od srednjih osovina nalazi na odstojanju

od srednjih osovina. Prema Van Hammeu, sleganje izvesnih određenih tačaka temelja nezavisno je od načina raspodele napona u temeljnom dnu. Za ove tačke sleganje se može izračunati uz pretpostavku, da je raspodela napona u temeljnom dnu ravnomerna. Za krutu temeljnu stopu, opterećenu ravnomernim opterećenjem po kod koje je raspodela napona u temeljnom dnu neravnomerna i raste prema ivicama stope, uprkos toga sleganje temeljne stope jednako je sleganju karakteristične tačke P. Naponi u dubini z ispod karakteristične tačke P pravougaone površine dužine a, širine b, opterećene ravnomernim opterećenjem p0 mogu se izračunati pomoću tablice 1 koju je izradio Jelinek.
Napon σzP u dubini z ispod karakteristične tačke P je σzP = (σz/p0)·p0, gde je p0 dopunsko opterećenje tla.
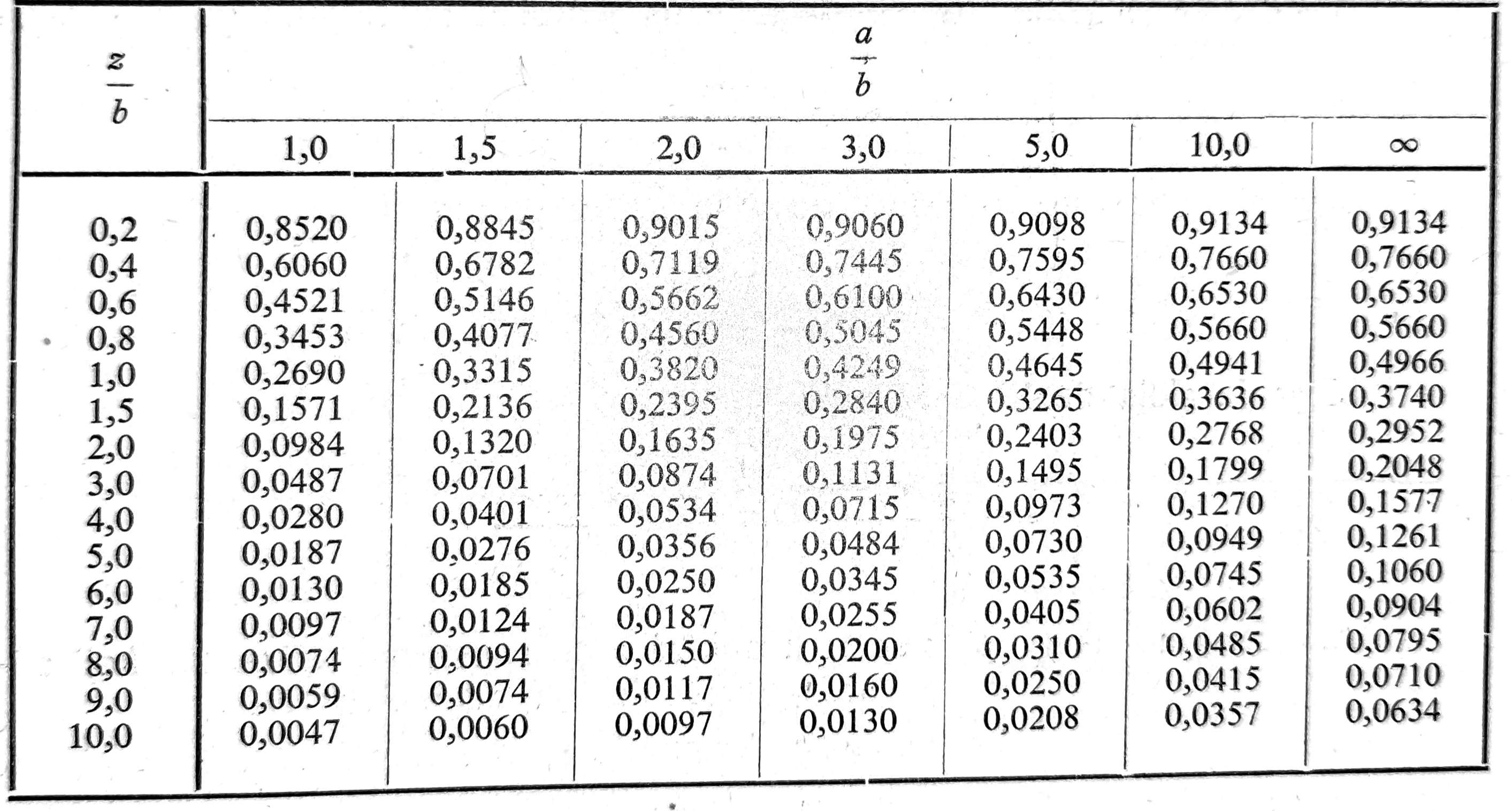
Tabl. 1. Vrednosti σz/p za napone ispod karakteristične tačke P u zavisnosti od odnosa dubine z prema širini b i od odnosa dužine a prema širini b temeljne stope
Proračun sleganja na bazi promene koeficijenza poroznosti tla
Ako označimo sa e0 koeficijent poroznosti neporemećenog uzorka izvađenog iz sloja tla, sa ei koeficijent poroznosti istog uzorka po završenoj konsolidaciji u edometru pod opterećenjem σ1 (sl. 4a), smanjenje početne zapremine tla pod dejstvom opterećenja Δσ odgovara smanjenju poroznosti odnosno koeficijentu poroznosti tla
Δe = e0 – e1
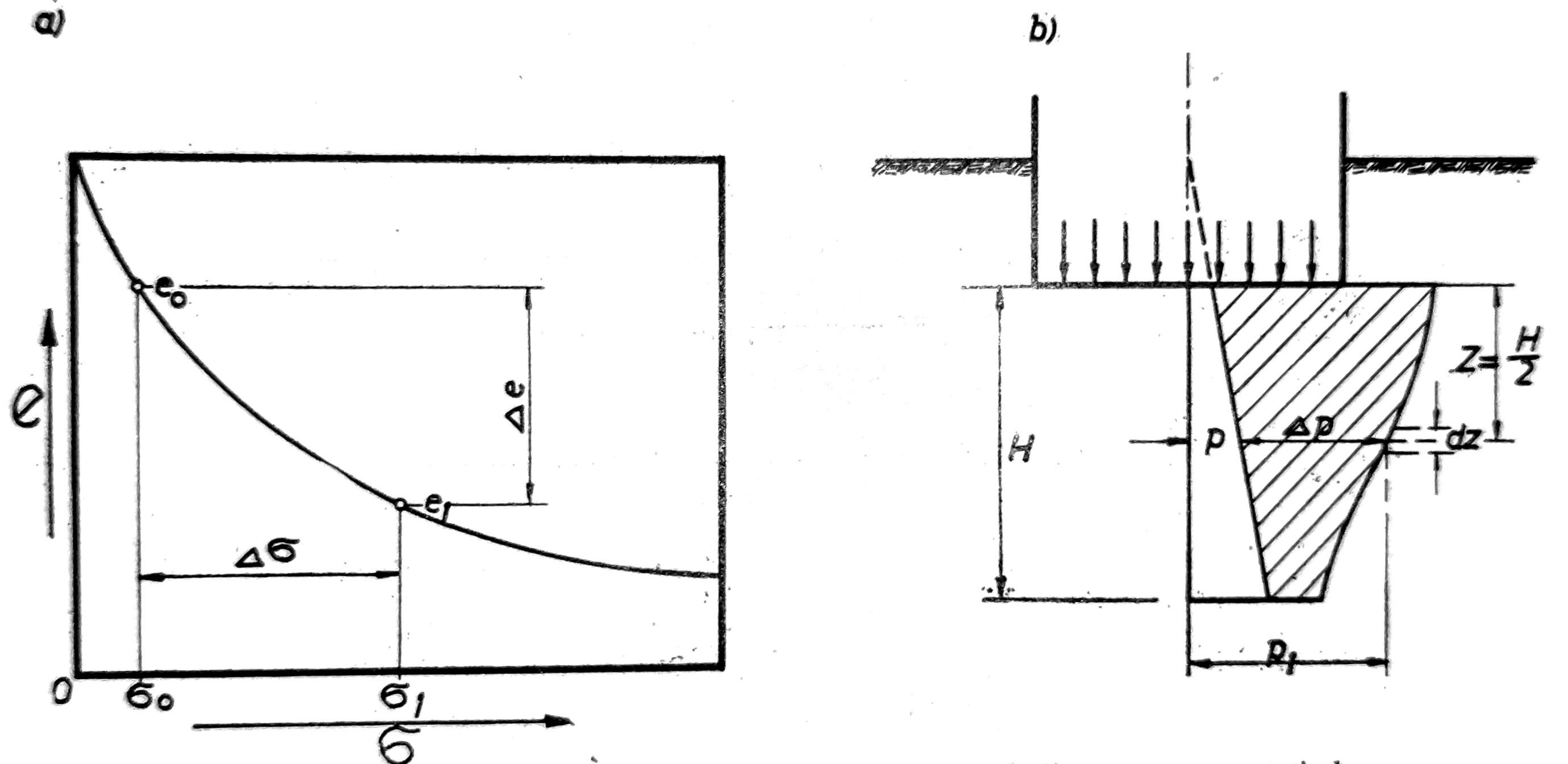
Sl. 4. Proračun sleganja na bazi promene koeficijenta poroznosti tla
Početna zapremina uzorka tla je
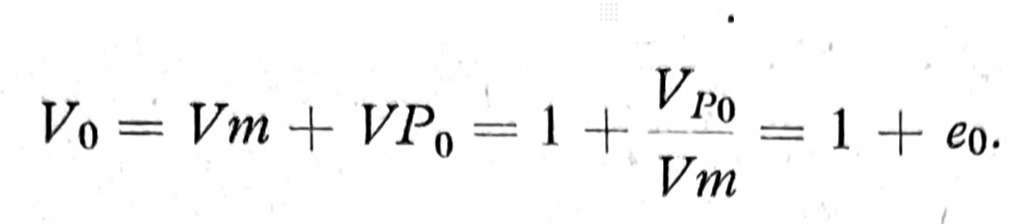
Specifično sleganje Δs, tj. sleganje na jedinicu zapremine tla 1+e0 je
Δs =(e0–e1) / (1+e0)
Sleganje elementarnog sloja debljine dz je prema sl. 4b
Δs dz=(e0–e1) / (1+e0) dz
Sleganje sloja debljine H biće
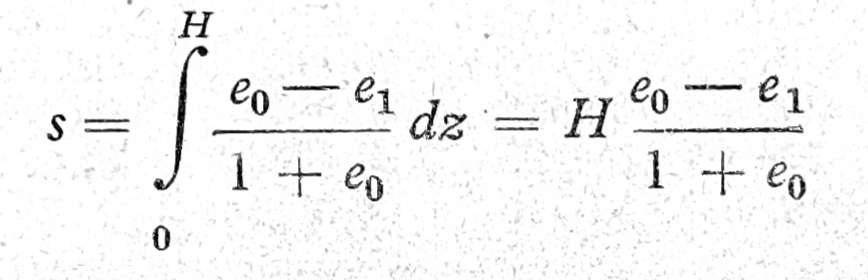
Ako stavimo da je p napon u dubini z od sopstevne težine tla, koji odgovara opterećenju σ0 u edometru, Δp napon od dopunskog opterećenja tla usled objekta, koji odgovara priraštaju opterećenja Δσ u edometru, p1 ukupan napon pod dejstvom sopstvene težine tla i dopunskog opterećenja koji odgovara ukupnom opterećenju σ1 u edometru, prednji obrazac možemo napisati u obliku
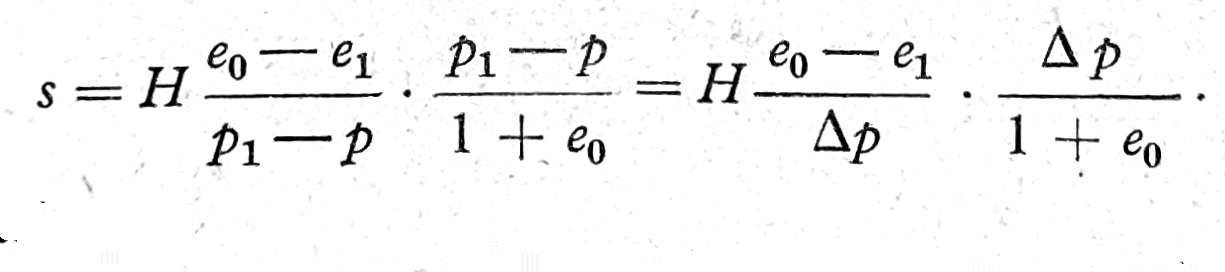
Ako označimo sa A površinu dijagrama napona od dopunskog opterećenja tla, A = ΔpH (šrafirana površina na sl. 4b), gde je Δp napon od dopunskog opterećenja u sredini sloja
a=Δe/Δp, odnos razlike koeficijenta poroznosti prema odgovarajućem naponu od dopunskog opterećenja Vc = (1+e0)/a, možemo staviti
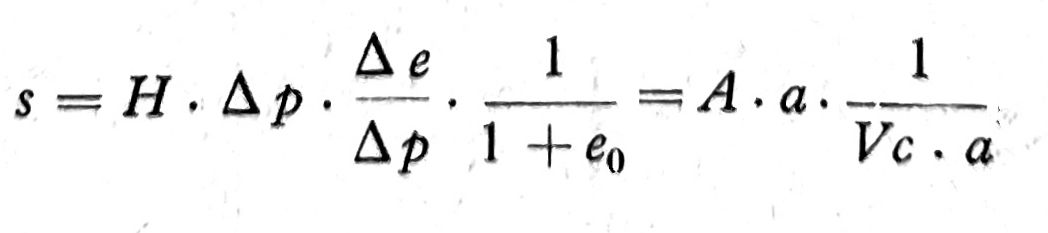
odnosno s = A/Vc [cm]
Ako se tlo sastoji iz više slojeva, izračunavaju se sleganja s za svaki sloj zbir sleganja pojedinačnih slojeva daje ukupno sleganje Σs.
